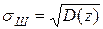Числовые характеристики случайных величин

Функция распределения и плотность распределения вероятностей являются наиболее полными характеристиками случайных величин. Однако во многих задачах практики оказывается трудно или даже невозможно полностью описать функцию распределения вероятностей.

В то же время для решения многих задач достаточно знать лишь некоторые параметры, характеризующие случайную величину с той или иной точки зрения. Наиболее распространёнными числовыми характеристиками (или моментами) случайных величин являются математическое ожидание и дисперсия, которые определяются следующими математическими выражениями:

Для дискретных случайных переменных, когда пространство исходов эксперимента Z является конечным множеством	Для непрерывных случайных переменных, когда пространство исходов эксперимента Z содержит бесконечное множество точек

Математическое ожидание является величиной, вокруг которой группируются значения случайной переменной. Дисперсия характеризует отклонение значений случайной величины от математического ожидания, то есть является характеристикой рассеивания случайной величины. Чем меньше дисперсия, тем более тесно группируются отдельные значения случайной величины вблизи математического ожидания.

Однако в ряде случаев дисперсия оказывается неудобной для практического использования, так как имеет размерность квадрата случайной величины. Поэтому в качестве характеристики рассеивания случайной величины часто используют корень квадратный из дисперсии, получивший название среднеквадратического отклонения

Отметим основные свойства дисперсии: дисперсия неслучайной величины равна нулю D(c) = M[(c-c)²] = 0; неслучайную величину можно вынести за знак дисперсии, возведя её в квадрат, D(cz)=M[(cz – cm_z)²] = c² × D(z).