Логический вывод в байесовских сетях доверия с непрерывными и дискретными состояниями

Логический вывод в таких БСД заключается в распространении вероятностей и параметров гауссовских законов распределения по всей сети в зависимости от полученных свидетельств. В частности, для рассматриваемого примера для исходного набора данных будут получены оценки производственных затрат:

m _п.з = 7483,33

s _п.з = 1208,1

Однако эти оценки могут быть пересчитаны для случая иной загрузки оборудования или получения новых свидетельств о ставках аренды или нормах амортизации. Наряду с этим возможен и обратный вывод в этой простейшей экспертной системе. Он, например, может заключаться в определении допустимых ставок арендных плат при возможном значении суммарных производственных затрат.

В основе процесса логического вывода лежат довольно сложные математические алгоритмы, которые мы рассмотрим на простейшей двухуровневой сети для случая прямого распространения распределения вероятностей.

Пусть независимые дискретные случайные величины X₁,..., X _s и непрерывные случайные величины Z₁,..., Z_r оказывают влияние на результирующую случайную величину Y.

 

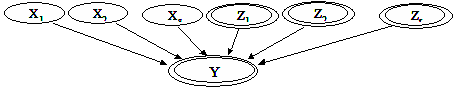
Каждая из дискретных случайных величин имеет своими исходами значения с вероятностями P_ij, для которых . Совместное влияние дискретных случайных величин на Y характеризуется математическим ожиданием и дисперсиями . Каждая из непрерывных случайных величин имеет непрерывное нормальное распределение с параметрами , где . Совместное влияние непрерывной случайной величины и исходов дискретных величин на результирующую случайную величину Y характеризуется весовыми коэффициентами для .

Тогда характеристики результирующей величины Y могут быть вычислены по следующим выражениям:

В частности, для рассмотренного выше примера, содержащего две исходные непрерывные (r=2) переменные и одну дискретную (s=1) переменную, имеющую три исхода (n₁=3), числовые характеристики случайной переменной «Производственные затраты» будут

0,333 × (3000 + 50000 × 0,075 + 0,6 × 2500) +

0,333 × (3200 + 40000 × 0,075 + 0,5 × 2500) +

0,333 × (3500 + 3000 × 0,075 + 0,4 × 2500) =

0,333 × (8250 + 7450 + 6750)= =7483,33

Полученные в результате математического расчета выводы полностью совпадают с результатами, выдаваемые системой Hugin для аналогичной модели БСД.