Пример построения простейшей диаграммы влияния
Вернёмся к ранее рассмотренному примеру с плантацией «яблочного Джека». Оценив ранее состояние своего дерева, Джек ставит перед собой цель принятия решения об инвестировании материальных средств в лечение дерева. Для решения этой задачи добавим к исходной байесовской сети доверия ещё три вершины шансов, полностью аналогичных тем, что уже были в байесовской сети доверия. Новые вершины: “ Болеет1”, “ Засохло1” и “ Облетело1” являются точно такими же как и их аналоги в предыдущей модели, но только отображают будущий момент времени (момент сбора урожая).
Рис.7.1. Расширенная модель БСД на момент уборки урожая. Новые вершины имеют те же состояния, что и старые. В новой модели ожидаются зависимости от “ Болеет ” к “ Болеет1 ” и от “ Засохло ” к “ Засохло1 ”. Это связано с тем, что если дерево болеет сейчас, очень вероятно, что оно будет болеть и в будущем. Конечно, сила зависимости зависит от того, как далеко в будущее мы хотим заглянуть. Можно было бы установить зависимость и от “ Облетело ” к “ Облетело1 ”, но в данной модели, для ее упрощения, мы этого делать не будем. «Яблочный Джек» имеет возможность сделать что-либо для решения проблемы опадания листвы со своих плодовых деревьев и, тем самым, сохранить урожай: · Он может попытаться лечить дерево, проводя его опрыскивание, чтобы избавить от болезни. · С другой стороны, если он считает, что опадание листвы вызвано засухой, он может сохранить свои деньги и просто ждать дождя. Действия, связанные с лечением дерева, могут быть добавлены в нашу модель в виде вершины решения и при этом мы от байесовской сети доверия переходим к диаграмме влияния, которая будет иметь вид:
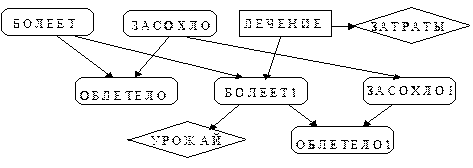
Рис.7.2. Преобразование БСД в диаграмму влияния добавлением в нее вершины решения. При этом случайная переменная решения, соответствующая вершине “ Лечение” может иметь два состояния (“ Лечение ” = «да», “ Лечение ” = «нет»). Как видно из рис.7.2, диаграмма влияния смоделирована со стрелкой от “ Лечение” к “ Болеет1”. Это вызвано тем, что лечение повлияет на будущее здоровье дерева. Перед тем как завершить диаграмму влияния, необходимо определить функцию полезности, позволяющую вычислить пользу от принятия решения. Это делается добавлением к диаграмме влияния вершин полезности, каждая из которых определяет вклад в общую выгодность. При этом изменённая диаграмма влияния примет вид, приведённый на рис.7.3.
Рис.7.3. Диаграмма влияния с добавленными вершинами полезности. Вершина “ Затраты ” содержит информацию о затратах на лечение деревьев, а вершина “ Урожай ” представляет собой доходы, полученные от сбора урожая. При этом естественно, что количество и качество урожая зависит от состояния деревьев. Поэтому вершина “ Урожай ” зависит от состояния вершины «Болеет1», указывая, что продукция зависит от здоровья дерева в момент сбора урожая. Модель, представленная на рис.7.3, даёт законченное качественное представление диаграммы влияния. Для получения количественного представления необходимо построить таблицу условных вероятностей для каждой из вершин шансов и задать таблицы доходности для каждой из вершин полезности. Вершины принятия решения не имеют таблиц условных вероятностей. При этом таблицы условных вероятностей для p (“ Болеет ”), p (“ Засохло ”) и p (“ Облетело ” | “ Болеет ”, “ Засохло ”),будут иметь тот же вид, что и в примере предыдущей главы. Таблица же условных вероятностей для p (“ Облетело1 ” | “ Болеет1”, “ Засохло1 ”), будет аналогична p (“ Облетело ” | “ Болеет ”, “ Засохло ”). Таблицы условных вероятностей для всех остальных состояний должны быть получены из анализа предметной области и выявления знаний от экспертов. Для рассматриваемого примера они могут иметь вид аналогичный, приведенным в табл. 7.1, 7.2, 7,3.
Следующие таблицы показывают как могут быть определены для рассматриваемого случая таблицы выгодности. В них функции полезности выражаются в виде стоимостных показателей и задаются в одних и тех же условных единицах.
Цель диаграммы влияния – вычислить действие, связанное с вершиной “ Лечение ” для того, чтобы получить наибольшую ожидаемую выгодность. Даже в таком простом примере ручной расчёт довольно-таки сложен и поэтому возникает необходимость работы с ЭС, такой, например, как “Hugin”. Ответом для принятия решения об инвестировании лечения будет вычисление общей функции полезности при условии, что p (“ Облетело ” = «облетело») = 1.
|