МОДУЛЬ 3.Расчет магнитных цепей постоянного тока.
Задано
Геометрические размеры ферромагнитного сердечника и кривая намагничивания материала сердечника. (Таблица 3.1.)
Требуется
a).Рассчитать магнитную цепь методом двух узлов и определить величины, указанные в крайнем справа столбце таблицы.
b) Для принятых в п.1 положительных направлений магнитных потоков и
заданного направления МДС составить систему уравнений по законам Кирхгофа.
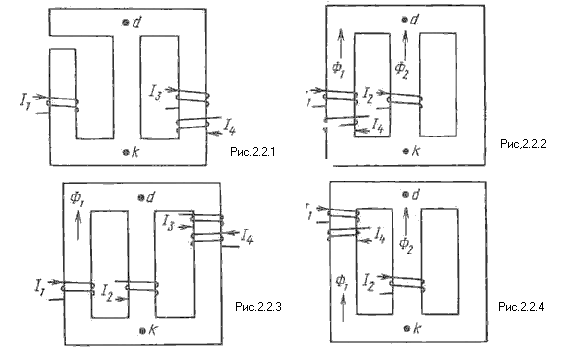
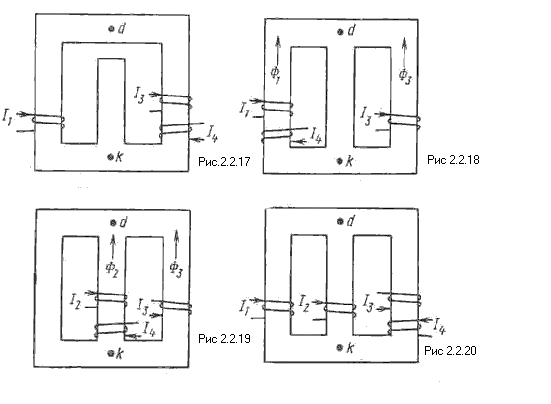
Схематические изображения магнитопроводов с размещением намагничивающих катушек, способа их намотки на сердечник и положительных направлений токов в них приведены на Рис.5.1. – 2.0.
Указания
В таблице 2.1 приняты следующие обозначения:
a) l – длина средней магнитной линии одной ветви магнитной цепи; lб – длина воздушного зазора (его положение в магнитной цепи дано на схемах магнитопроводов);
b) s- сечение участков магнитопровода; w – число витков катушек; I – постоянный ток в катушке.
c) Обозначения величин даются с индексами, которые указывают, к какой ветви магнитной цепи относится та или иная величина; индекс 1 – к левой магнитной ветви; 2 – к средней ветви; 3 - к правой ветви.
d) Магнитные свойства стали, из которой изготовлены магнитопроводы, определяются кривой намагничивания, которая дана в следующей таблице:
| Н.А/м
|
|
|
|
|
|
|
|
|
|
| | В. Тл
| 0,22
| 0,75
| 0,93
| 1,02
| 1,14
| 1,28
| 1,47
| 1,53
| 1,57
| 1,6
| 
| Вариант
| Рисунок
2,2,
| Дано
| | l1,
см
| S1,
см2 
| ω1
| I1, А
| l2,
см
| S2,
см2
| ω2
| I2,
А
| l3,
см
| |
|
|
| 4,00
|
| 1,52
| 10,0
| 6,0
| ---
| ---
| 30,0
| |
|
| 100.
| 6,15
|
| 0,30
| 33,0
| 4,2
|
| ----
|
| |
|
| 30,0
| 4,3
|
| 0,10
| 12,0
| 6,0
|
| ---
| 20,0
| |
|
| 30,0
| 7,3
|
| 1,00
| 11,5
| 12,3
|
| 0,30
| 22,5
| |
|
| 32,0
| 14,4
|
| 0,75
| 25,0
| 10,5
| ----
| ---
| 40,0
| |
|
| 40,0
| 42,0
|
| 0,40
| 13,0
| 14,0
| ----
| 0,30
| 40,0
| |
|
| 30,0
| 4,2
|
| 0,50
| 10,0
| 4,8
| ----
| 0,10
| 32,0
| |
|
| 19,0
| 8,1
|
| 0,15
| 6,5
| 5,1
|
| 0,10
| 15,0
| |
|
| 55,0
| 55,0
|
| 1,00
| 18,0
| 84,0
| ---
| ---
| 57,0
| |
|
| 55,0
| 25,3
|
| 0,50
| 25,0
| 50,0
| ---
| ---
| 47,0
| |
|
| 11,0
| 1,95
|
| -----
| 3,5
| 0,96
|
| 0,05
| 13,0
| |
|
| 35,0
| 2,9
|
| 0,25
| 10,0
| 4,75
|
| ---
| 45,0
| |
|
| 13,5
| 7,5
| ----
| ----
| 4,32
| 1,9
|
| 1,00
| 19,8
| |
|
| 30,0
| 5,6
|
| 0,20
| 10,0
| 5,0
|
| ---
| 18,0
| |
|
| 28,0
| 7,95
|
| 0,50
| 11,5
| 13,8
|
| 1,00
| 37,0
| |
|
| 28,0
| 3,9
|
| 0,50
| 8,0
| 6,8
|
| ---
| 28,0
| |
|
| 25,0
| 8,0
|
| 1,10
| 10,0
| 5,0
| ---
| 1,10
| 25,0
| |
|
|
|
|
| 0,4
|
|
|
| 1,4
|
| |
|
|
| 11,9
| -
| -
|
| 11,5
|
|
|
| |
|
|
| 9,3
|
| 0,06
|
| 7,7
| -
| 0,2
|
| |
|
|
|
|
| 0,9
|
| 6,15
| -
| -
|
| |
|
|
|
|
| 0,3
|
|
|
| -
|
| |
|
| 4,5
|
| 4,15
|
| 0,2
| 8,4
|
| -
|
| |
|
|
|
|
| 0,5
| 22,5
|
|
| 0,1
|
| |
|
|
|
|
| 0,5
|
| 10,3
| -
| -
|
| |
|
|
|
|
|
|
| 13,7
| -
| 0,3
|
| |
|
|
| 4,3
|
|
|
| 4,8
| -
| 0,1
|
| |
|
|
| 7,8
|
| 0,3
| 5,5
| 4,9
|
| 0,07
|
| |
|
|
|
|
| 0,5
|
|
| -
| -
|
|
| Вариант
| Дано
|
Дополнительные условия, Ф∙10 -5
|
Определить
| | S3,
см2
| ω3
| I3,
A
| ω4
| I4,
А
| ld,
см
| |
| 4,0
|
| 2,5
|
| 2,5
| 0,5
| ------
| Ф2, Ф1
| |
| 10,0
| ---
| -
|
| 0,3
| -
| Ф1=Ф2
| I2,Ф3
| |
| 4,8
|
| 0,42
|
| 0,21
| -
| Ф2= 0
| I2,Ф3
| |
| 10,0
|
| -
|
| 0,15
| -
| Ф3-Ф1= 20
| I3, Ф1
| |
| 15,0
|
|
|
| 1,5
|
| ------
| Ф2,Ф3
| |
| 15,0
| ---
| -
|
| 0,5
| -
| Ф2=Ф3
| ω2, Ф3
| |
| 4,9
|
| 0,5
|
|
| -
| Ф2= 0
| ω2, Ф1
| |
| 3,2
|
| -
|
| 0,1
| -
| Ф2-Ф3= 20
| I3, Ф1
| |
| 57,0
|
| 1,0
|
| 0,5
| 1,25
| -------
| Ф2,Ф3
| |
| 45,5
|
| -
|
|
| -
| Ф1=Ф3
| I3, Ф3
| |
| 1,25
|
| 0,3
|
| 0,155
| -
| Ф1 =25
| I1, Ф2
| |
| 8,33
| ---
| -
|
| 0,5
| -
| Ф3-Ф1= 20
| I2, Ф1
| |
| 1,75
|
| 0,5
|
| 0,25
| 0,1
| ----------
| Ф3, Ф1
| |
| 8,9
| ---
| -
|
| 0,1
| -
| Ф1=Ф2
| I2,Ф3
| |
| 7,1
|
| -
|
| 0,5
| -
| Ф3=98
| I3, Ф2
| |
| 9,9
|
| 0,25
|
| 0,125
| -
| Ф2-Ф1= 20
| I2, Ф2
| |
| 3,0
|
| 0,2
|
| 0,1
| -
| Ф2=70
| ω2, Ф3
| |
|
| -
| -
|
| 0,4
| 0,57
| ------
| Ф2,Ф3
| |
| 9,1
|
| -
|
| 0,55
| -
| Ф2=Ф3
| I3, Ф1
| |
| 15,5
|
| 0,7
|
| 0,35
| -
| Ф2-Ф1 =30
| ω2, Ф2
| |
| 3,9
|
| 0,2
|
| 0,2
| 0,5
| -
| Ф2,Ф3
| |
| 9,7
| -
| -
|
| 0,2
| -
| Ф1=Ф2
| I2,Ф3
| |
| 5,95
|
| 0,525
|
| 0,525
| -
| Ф2 =0
| I2,Ф1
| |
|
|
| -
|
| 0,4
| -
| Ф3-Ф1 =20
| I3, Ф3
| |
|
|
| 0,25
|
|
|
| -
| Ф3, Ф1
| |
| 14,2
| -
| -
|
|
| -
| Ф2=Ф3
| ω2, Ф2
| |
| 4,4
|
| 0,1
|
| 0,2
| -
| Ф2 =0
| ω2, Ф1
| |
| 4,2
|
| -
|
| 0,6
| -
| Ф2-Ф3 =20
| I3, Ф3
| |
|
|
| 0,5
|
|
| 1,25
| -
| Ф2,Ф1
| | | | | | | | | | | |
| Вариант
| Рисунок
2,2,
|
| | l1,
см
| S1,
см2
| ω1
| I1, А
| l2,
см
| S2,
см2
| ω2
| I2,
А
| l3,
см
| |
|
|
| 24,9
|
|
|
| 51,5
| -
| -
|
| |
|
|
| 2,05
|
| -
|
| 0,94
|
| 0,02
|
| |
|
|
| 3,1
|
| 0,3
|
| 5,3
|
| -
|
| |
|
| 19,5
| 7,7
| -
| -
|
| 2,1
|
| 0,5
| 24,2
| |
|
|
| 4,9
|
| 0,25
|
|
| -
| 0,2
| 0,25
| |
|
|
| 7,9
|
|
|
| 13,6
| 5,2
| 0,5
|
| |
|
|
| 4,1
|
|
|
| 6,3
|
| -
|
| |
|
|
| 7,7
|
| 0,59
|
| 4,9
| -
| 0,1
|
| |
|
|
|
|
|
|
|
|
| 2,8
|
| |
|
|
| 11,8
| -
| -
|
|
|
| 2,2
|
| |
|
|
| 9,5
|
| 0,1
|
|
| -
| 0,2
|
| |
|
|
| 4,1
|
| 1,3
|
| 5,8
| -
| -
|
| |
|
|
|
|
| 1,2
|
|
| -
| 1,1
|
| |
|
|
| 3,8
|
| 0,5
|
|
|
| -
|
| |
|
| 37,5
| 7,8
|
| 0,53
|
| 12,8
|
| 0,2
| 37,5
| |
|
|
| 14,6
|
| 0,3
|
| 10,2
| -
| -
|
| |
|
|
|
|
| 0,25
|
| 14,7
| -
| 0,3
|
| |
|
|
|
|
| 0,2
|
| 4,8
| -
| 0,1
|
| |
|
|
| 8,2
|
| 0,1
|
| 5,2
|
| 0,2
|
| |
|
|
|
|
| 1,3
| 1,9
|
| -
| -
|
| |
|
|
| 24,7
|
| 0,5
|
| 50,4
| -
| -
|
| |
|
|
| 1,92
|
| -
| 4,5
| 1,02
|
| 0,1
|
| |
|
|
| 2,97
|
| 0,15
| 1,1
| 4,9
|
| -
|
| |
|
| 29,8
| 8,2
| -
| -
|
| 2,2
|
| 0,1
|
| |
|
|
|
|
| 0,4
|
|
|
| -
|
| |
|
|
| 8,1
| 7,25
| 0,2
|
| 14,1
|
| 0,3
|
| |
|
|
|
|
| 0,5
|
|
|
| -
|
| |
|
|
| 8,4
|
| 0,73
|
| 5,2
| -
| 0,1
|
| |
|
|
|
|
| 0,5
|
|
|
|
|
| |
|
|
| 12,1
| -
| -
|
| 12,9
|
|
|
|
| Вариант
| Дано
|
Дополнительные условия, Ф∙10 -5
|
Определить
| | S3,
см2
| ω3
| I3,
A
| ω4
| I4,
А
| ld,
см
| |
| 51,5
|
| -
|
| 0,25
| -
| Ф1=Ф3
| I3, Ф2
| |
| 1,18
|
| 0,15
|
| 0,1
| -
| Ф1 =25
| I1, Ф3
| |
| 7,8
| -
| -
|
| 0,15
| -
| Ф2-Ф1 =20
| I2, Ф2
| |
| 1,8
|
| 0,2
|
| 0,4
| 0,1
| -
| Ф2, Ф1
| |
| 9,5
| -
| -
|
| 0,25
| -
| Ф1=Ф2
| ω2, Ф1
| |
| 7,2
|
| -
|
| 0,5
| -
| Ф3 =98
| I3, Ф2
| |
| 9,6
|
| 0,2
|
| 0,2
| -
| Ф2-Ф1 =20
| I2, Ф3
| |
|
|
| 0,7
|
| 0,35
| -
| Ф2 =70
| ω2, Ф3
| |
|
| -
| -
|
| 0,5
| 0,48
| -
| Ф3, Ф1
| |
| 9,3
|
| -
|
| 1,1
| -
| Ф2=Ф3
| I3, Ф2
| |
| 15,6
|
| 2,5
|
| 1,25
| -
| Ф2-Ф1 =30
| ω2, Ф3
| |
| 3,8
|
| 0,5
|
| 0,5
| 0,5
| -
| Ф2, Ф1
| |
| 9,7
| -
| -
|
| 0,6
| -
| Ф1=Ф2
| ω2, Ф2
| |
| 4,8
|
| 0,3
|
| 0,08
| -
| Ф2 =0
| I2, Ф1
| |
| 10,5
|
| -
|
| 0,25
| -
| Ф3-Ф1 =20
| I3, Ф2
| |
|
|
| 0,2
|
| 0,5
|
| -
| Ф3, Ф1
| |
| 15,4
| -
| -
|
| 0,5
| -
| Ф2=Ф3
| ω2, Ф3
| |
| 4,8
|
| 0,05
|
| 0,2
| -
| Ф2 =0
| ω2, Ф3
| |
| 3,6
|
| -
|
| 0,05
| -
| Ф2-Ф3 =20
| I3, Ф1
| |
|
|
| 0,4
|
| 0,8
| 1,25
| -
| Ф2, Ф1
| |
| 47,5
|
| -
|
|
| -
| Ф1=Ф3
| I3, Ф1
| |
| 1,26
|
| 0,2
|
| 0,1
| -
| Ф1 =25
| I1, Ф2
| |
| 8,25
| -
| -
|
| 0,3
| -
| Ф2-Ф1 =20
| I2, Ф3
| |
| 1,82
|
| 0,75
|
| 1,5
| 0,1
| -
| Ф2, Ф3
| |
|
| -
| -
|
| 0,2
| -
| Ф1=Ф2
| I2, Ф2
| |
| 6,9
|
| -
|
| 0,15
| -
| Ф3 =98
| I3, Ф1
| |
|
|
| 0,2
|
| 0,1
| -
| Ф2-Ф1 =20
| I2, Ф2
| |
|
|
| 0,4
|
| 0,2
| -
| Ф2 =70
| ω2, Ф1
| |
|
| -
| -
|
|
| 0,46
| -
| Ф2, Ф1
| |
| 8,8
|
| -
|
| 0,5
| -
| Ф2=Ф3
| I3, Ф1
| | | | | | | | | | | |
| Вариант
| Рисунок
2,2,
|
| | l1,
см
| S1,
см2
| ω1
| I1, А
| l2,
см
| S2,
см2
| ω2
| I2,
А
| l3,
см
| |
|
|
| 8,6
|
| 0,14
|
| 8,1
| -
| 0,2
|
| |
|
|
| 4,1
|
|
|
|
| -
| -
|
| |
|
|
| 5,9
|
|
|
| 3,9
| -
| 1,1
| 9,5
| |
|
|
| 4,3
|
| 0,15
|
|
|
| -
|
| |
|
|
|
|
| 0,25
|
|
|
| 0,2
|
| |
|
|
| 15,6
|
| 0,2
|
| 10,3
| -
| -
|
| |
|
|
|
|
| 0,3
|
| 13,8
| -
| 0,3
|
| |
|
|
| 3,8
|
| 0,25
|
| 4,8
| -
| 0,1
|
| |
|
|
|
|
| 0,2
|
|
|
| 0,1
|
| |
|
|
| 66,5
|
| 0,4
|
|
| -
| -
|
| |
|
|
| 25,2
|
| 0,35
|
|
| -
| -
|
| |
|
|
| 2,07
|
| -
|
| 1,03
|
| 0,2
|
| |
|
|
| 3,07
|
| 0,1
|
| 5,14
|
| -
|
| |
|
| 42,5
|
| -
| -
|
| 2,4
|
|
| 40,5
| |
|
|
|
|
| 0,12
|
|
| -
| 0,2
|
| |
|
|
| 8,3
|
| 0,5
|
| 14,2
|
| 0,2
|
| |
|
|
| 4,06
|
| 0,25
|
| 8,3
|
| -
|
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
ПУНКЦИЯ И КАТЕТЕРИЗАЦИЯ ПОДКЛЮЧИЧНОЙ ВЕНЫ
Пункцию и катетеризацию подключичной вены обычно производит хирург или анестезиолог, иногда — специально обученный терапевт...
Ситуация 26. ПРОВЕРЕНО МИНЗДРАВОМ
Станислав Свердлов закончил российско-американский факультет менеджмента Томского государственного университета...
Различия в философии античности, средневековья и Возрождения ♦Венцом античной философии было: Единое Благо, Мировой Ум, Мировая Душа, Космос...
|
Подкожное введение сывороток по методу Безредки. С целью предупреждения развития анафилактического шока и других аллергических реакций при введении иммунных сывороток используют метод Безредки для определения реакции больного на введение сыворотки...
Принципы и методы управления в таможенных органах Под принципами управления понимаются идеи, правила, основные положения и нормы поведения, которыми руководствуются общие, частные и организационно-технологические принципы...
ПРОФЕССИОНАЛЬНОЕ САМОВОСПИТАНИЕ И САМООБРАЗОВАНИЕ ПЕДАГОГА Воспитывать сегодня подрастающее поколение на современном уровне требований общества нельзя без постоянного обновления и обогащения своего профессионального педагогического потенциала...
|
|
