Выравнивание по прямой.
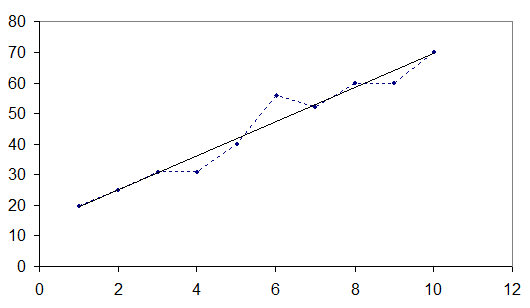
Предположим, что точки (хi уi) группируются около некоторой прямой.
рис 1.
В этом случае между переменными X и У существует функциональная зависимость, близкая к линейной. Будем искать эту зависимость в виде:
где a и b – параметры, подлежащие, вычислению,
Поставим задачу: найти такие значения а и b, чтобы прямая (1.1.) «наилучшим образом» проходила через множество точек Мi (xi, yi). Если бы все точки Mi(xi, yi) лежали строго на прямой (1.1), то для каждой из точек было бы справедливо следующее равенство:
однако на практике имеет место следующее равенство:
т.е существует Принцип метода наименьших квадратов утверждает: оптимальны такие значения параметров а и b при которых сумма квадратов отклонений минимальна. Составим эту сумму:
Для исследования функции (1.3) с двумя переменными на минимум, найдем частные производные, приравняем их к нулю и решив систему уравнений, найдем а и b.
или
Введя сокращенные обозначения, получим систему уравнений (1.5) в следующем виде:
Решив систему (1.6), найдем значения параметров а и b и подставим их значения в эмпирическую формулу (1.1). Нахождение линейной функциональной зависимости называется выравнивание по прямой, а система уравнений (1.6) - нормальной системой метода наименьших квадратов при выравнивании по прямой.
|

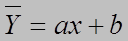 (1.1)
(1.1)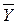 - теоретическое значение функции (вычисленное по формуле).
- теоретическое значение функции (вычисленное по формуле).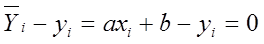
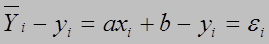 (1.2)
(1.2)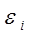 (отклонение) между наблюдаемыми ординатами (эмпирическими) и ординатами, полученными по уравнению (теоретическими).
(отклонение) между наблюдаемыми ординатами (эмпирическими) и ординатами, полученными по уравнению (теоретическими).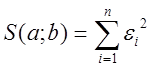 или
или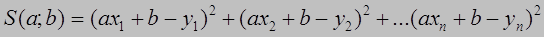 (1.3)
(1.3)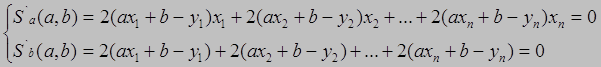 (1.4)
(1.4)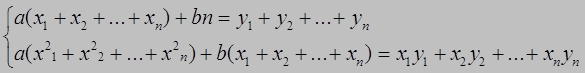 (1.5)
(1.5)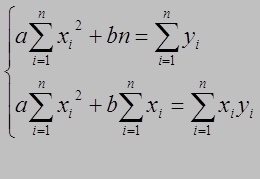 (1.6)
(1.6)


