Задачи надежности в ТЭА
Цель занятия. Освоение методов решения задач связанных со свойства надежности в ТЭА.
Надежность – свойство системы сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах применения, технического обслуживания, ремонта, хранения и транспортирования. Надежность – сложное комплексное, четко регламентируемое (на уровне ГОСТа) свойство системы. Надежность как комплексное свойство системы определяется совокупностью четырех белее простых свойств, а именно: безотказностью, долговечностью, ремонтопригодностью и сохраняемостью. Причем в зависимости от особенностей конструкции и функционирования системы то или иное свойство (или свойства) в состав надежности может не входить. Безотказность – свойство системы непрерывно сохранять работоспособное состояние при функционировании в течение некоторого (заданного) времени или некоторой (заданной) наработки. Долговечность – свойство системы функционировать до предельного состояния при установленном порядке технического обслуживания и ремонта. Ремонтопригодность – свойство системы, заключающееся в приспособленности к предупреждению и обнаружению предотказных состояний, отказов и повреждений, поддержанию и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонта. Сохраняемость – свойство системы сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение и после хранения и (или) транспортировки.
Задача № 1
Определить вероятность первой замены детали при работе автомобиля с начала эксплуатации до наработки Решение.
Дополнение к зад. 1. а) Определить вероятность безотказной работы при пробеге Решение.
б) Определить
1. где
2.
Задача № 2 Определить вероятность отказа той же детали в интервале пробега от Решение. 1. Вероятность отказа детали в заданном диапазоне –
Задача № 3.
Наработка до первой замены накладок сцепления
Решение. Необходимо найти накопленное число отказов (первого и последующих) к наработке
Здесь
т.е. к пробегу
Задача № 4 Определить для условий предыдущей задачи 3 с доверительной вероятностью Решение. Это задача по расчету гарантированных запасов. Для ее решения необходимо провести интервальную оценку ведущей функции параметра потока отказов. Для достаточно больших x имеем:
где
Таким образом, с доверительной вероятностью 0,9 можно полагать, что за
|

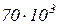 км. Распределение наработки до первого отказа подчиняется нормальному закону с параметрами
км. Распределение наработки до первого отказа подчиняется нормальному закону с параметрами  км,
км, 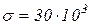 км.
км.
 т.е. вероятность первой замены детали при пробеге
т.е. вероятность первой замены детали при пробеге  %
% км
км
 –процентную наработку до отказа для
–процентную наработку до отказа для  и
и  .
. ,
,  ,
, –
–  квантиль распределения наработки до первого отказа.
квантиль распределения наработки до первого отказа. ;
;  .
.  .
. .
. 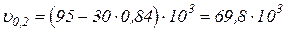 .
.  .
. .
. .
. ;
;  .
. 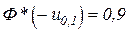 .
. .
.  .
.  км.
км. км до
км до 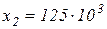 км.
км.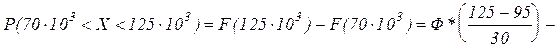
 .
. .
. км;
км; 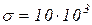 км; коэффициент восстановления ресурса
км; коэффициент восстановления ресурса  . Определить возможное число замен накладок при пробеге
. Определить возможное число замен накладок при пробеге  км, считая, что наработка до отказа распределена по нормальному закону.
км, считая, что наработка до отказа распределена по нормальному закону. км, т.е. найти ведущую функцию потока отказов
км, т.е. найти ведущую функцию потока отказов  .
. ;
;  .
. – число отказов (замен).
– число отказов (замен).





 ;
;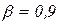 необходимое число накладок сцепления на пробег в
необходимое число накладок сцепления на пробег в  ,
,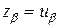 – квантиль уровня
– квантиль уровня  для стандартного нормального распределения.
для стандартного нормального распределения. .
.
 .
.


