Формы задания законов распределения случайных величин
Случайной называется величина, принимающая в результате испытания числовое значение, которое принципиально нельзя указать исходя из условий событий. Случайная величина обладает целым набором допустимых значений, но в результате каждого отдельного испытания принимает лишь какое-то одно из них. Чтобы охарактеризовать случайную величину, необходимо задать набор ее допустимых значений. В зависимости от того каков набор, этих значений различают непрерывные и дискретные случайные величины. Случайная величина называется дискретной, если между любыми двумя ее значениями заключено лишь конечное число других допустимых значений. Если же возможные значения случайной величины заполняют непрерывно промежуток между любыми двумя ее значениями, то такая случайная величина непрерывная. Случайные величины будут, обозначаться большими буквами, а их возможные значения – соответствующими малыми. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Простейшей формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения этой величины и соответствующие им вероятности.
Такую таблицу называют рядом распределения случайной величины. Графическое представление ряда распределения, имеющее вид рис. 1, называют многоугольником распределения.
Рис. 1
Функция распределения Ряд распределения, давая исчерпывающую характеристику дискретной случайной величине, не может быть использован для задания непрерывной случайной величины. Для количественной характеристики распределения вероятностей непрерывной величины надо пользоваться не вероятностью события Функцию распределения называют также интегральной функцией или интегральным законом распределения. Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин – дискретных и непрерывных, являясь одной из форм закона распределения. Обычно функция распределения непрерывной случайной величины представляет собой функцию, непрерывную во всех точках. Однако можно найти пример случайных величин, возможные значения которых непрерывно заполняют некоторый промежуток, но для которых функция распределения не везде непрерывна, а в отдельных точках терпит разрывы. Такие случайные величины называются смешанными.
Плотность распределения Функция распределения, увеличиваясь от значения к значению, является функцией "накопленной" вероятности и не дает простого и наглядного представления о законе распределения случайной величины. Этого недостатка лишена функция
Функция
Рис. 2 Плотность распределения как и функция распределения есть одна из форм задания закона распределения. Эта форма более удобна и наглядна, однако она существует только для непрерывных случайных величин. С помощью плотности распределения легко вычислить вероятность попадания случайной величины на заданный участок. Если это элементарный участок По плотности распределения легко найти функцию распределения: Основные свойства плотности распределения. 1. Плотность распределения есть неотрицательная функция т.к. 2. Интеграл в бесконечных пределах от плотности распределения равен 1.
Геометрически основные свойства плотности распределения означают, что: ¾ во-первых вся кривая распределения лежит не ниже оси абсцисс; ¾ во-вторых полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Числовые характеристики случайных величин
Ранее в качестве характеристик случайных величин были рассмотрены: - для дискретной случайной величины: функция распределения; ряд распределения (графически – многоугольник распределения); - для непрерывной случайной величины: функция распределения; плотность распределения (графически – кривая распределения). Каждый закон распределения представляет собой некоторую функцию, и указание этой функции полностью описывает случайную величину с вероятностной точки зрения. Однако во многих случаях нет необходимости определять случайную величину исчерпывающим образом. Достаточно бывает указать только отдельные числовые параметры, характеризующие основные особенности распределения случайной величины. Пользуясь такими характеристиками, можно выразить все существенные сведения о случайной величине более компактно, с помощью минимального числа параметров. Такие характеристики, назначение которых – выразить в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины.
|



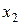


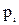
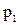
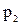

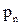

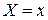 , а вероятностью события
, а вероятностью события 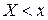 , где x – некоторая текущая переменная. Вероятность этого события зависит от x и есть некоторая функция от x. Эта функция называется функцией распределения случайной величины X и обозначается
, где x – некоторая текущая переменная. Вероятность этого события зависит от x и есть некоторая функция от x. Эта функция называется функцией распределения случайной величины X и обозначается 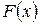 .
. 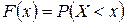 .
.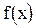 , называемая плотностью распределения или плотностью вероятности, или дифференциальной функцией распределения случайной величины X. Для получения ее рассмотрим вероятность попадания случайной величины X на участок
, называемая плотностью распределения или плотностью вероятности, или дифференциальной функцией распределения случайной величины X. Для получения ее рассмотрим вероятность попадания случайной величины X на участок 
 . Найдем теперь среднюю вероятность, приходящуюся на единицу длины этого участка, а сам участок будет стягивать в точку за счет
. Найдем теперь среднюю вероятность, приходящуюся на единицу длины этого участка, а сам участок будет стягивать в точку за счет  :
: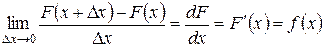 .
.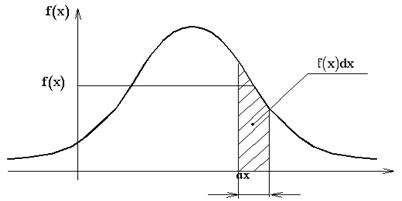
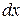 , то искомая вероятность равна
, то искомая вероятность равна 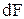 и в соответствии с рис.2 равна
и в соответствии с рис.2 равна 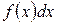 . Величина
. Величина 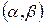 равна интегралу от элемента вероятности
равна интегралу от элемента вероятности  .
.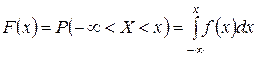 .
.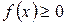
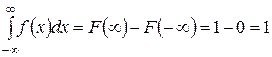 .
.


