В) Свойства квантилей нормального распределения.
Первое свойство. Симметричность. Пусть p<0,5. Тогда Теперь найдем квантиль Таким образом,
Задача № 3
Показать симметричность квантилей u0,25 и u0,75. Решение. x=0,675. u0,25=–0,675.
x=0,675. u0,75=0,675. Второе свойство. Возможность определения попадания на заданный интервал. Задача № 4
Определить вероятность попадания стандартной нормально распределенной величины на интервал – 0,6¸0,8. Решение.
2. Понятие доверительного интервала и доверительной вероятности.
Равенство означает, что с вероятностью b неизвестные значения параметра а попадает в интервал
3. Использование квантилей для определения границ доверительного интервала.
Использование второго свойства квантилей позволяет по заданной доверительной вероятности Тогда, по второму свойству
Задача № 5
Найти границы доверительного интервала, если случайная величина распределена по нормальному закону с промежутками Решение. 1. Определение уровней квантилей.
2. Определение границ доверительного интервала для стандартной случайной величины.
3. Определение границ доверительного интервала для исходной случайной величины:
|

 , где x – решение уравнения
, где x – решение уравнения  .
. . Так как
. Так как  , то
, то  , где x – решение уравнения
, где x – решение уравнения  , т.е. квантили up и u1–p – симметричны.
, т.е. квантили up и u1–p – симметричны. , где x – решение уравнения
, где x – решение уравнения 
 , где x –решение уравнения
, где x –решение уравнения  ;
; .
. ,
,  .
.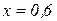 ;
;  ,
,  .
. ;
;  ,
,  .
. .
. .
.
 . В данном случае величина а не случайна, но случаен интервал
. В данном случае величина а не случайна, но случаен интервал  . При этом b следует толковать как вероятность того, что случайный интервал
. При этом b следует толковать как вероятность того, что случайный интервал 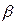 определить границы доверительного интервала
определить границы доверительного интервала  , то правая граница
, то правая граница  .
. ;
;  ;
;  ;, а следовательно, по полученным значениям
;, а следовательно, по полученным значениям  и
и 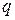 легко будут найдены величины
легко будут найдены величины 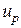 и
и  – границы доверительного интервала.
– границы доверительного интервала. ,
,  , а доверительная вероятность
, а доверительная вероятность  .
.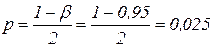


 .
. 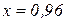 .
.  .
.
 .
.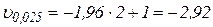 .
.  .
.


