Нормальный закон распределения
Цель занятия. Изучение законов распределения случайной величины и их физический смысл на примере решения задач для нормального закона распределения.
Случайные величины в зависимости от их физического смысла могут иметь различные законы распределения. В теории вероятностей известно большое число таких законов. Однако рассматривать количественные характеристики имеет смысл только для ограниченного их числа. Это объясняется тем, что интересующие исследователя величины (в данном случае это показатели надежности) подчиняются определенным и немногим законам распределения. Такими законами могут быть: экспоненциальный (показательный); Рэлея; нормальный; гамма–распределение; Вейбулла. Из перечисленных законов особая роль принадлежит нормальному (закону Гаусса). Нормальный закон является предельным законом, к которому приближаются другие законы распределения при часто вращающихся типичных условиях. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений могут быть представлены как суммы большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Нормальное распределение является наиболее изученным распределением. Поэтому его стараются использовать и при изучении случайных величин, распределения которых отличны от нормального. Здесь могут быть два основных пути. Первый путь заключается в переходе по определенной формуле, которую вследствие можно будет учесть, от заданной величины к другой, имеющей нормальное распределение. Например, при изучении случайной величины X может оказаться, что нормальное распределение имеет ее логарифм, т.е. Второй путь заключается в приближенной замене распределения исследуемой случайной величины нормальным. Он особенно часто применяется при обработке экспериментальных данных, где, как правило, нет возможности установить распределение случайной величины с абсолютной точностью. 1. Нормальный закон распределения и его роль при изучении физических явлений.
Параметры распределения m и s имеют совершенно определенный смысл: m – математическое ожидание, а s – среднее квадратическое отклонение величины распределенной по нормальному закону.
2. Вероятность попадания нормально распределенной случайной величины на заданный интервал. Наиболее распространенной задачей, связанной с нормально распределенными случайными величинами, является определение вероятности попадания такой величины на участок Так как Х распределена по нормальному закону с плотностью Полученный интеграл не выражается через элементарные функции, но его можно выразить через специальные функции, значения которых заранее вычислены и сведены в таблицы. Наиболее распространенной специальной функцией, используемой для этого, является функция вида
Задача № 1 Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 м. Среднее квадратическое отклонение ошибки измерения равно 0,8м. Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 м. Решение.
Параметры распределения m=1,2;
Задача № 2
Найти ту же вероятность, что и в предыдущей задаче (задача №1), но при условии, что систематической ошибки нет. Решение.
Задача № 3
Техническими условиями задано, что длина детали должна лежать между 24 и 25 см. Длина детали – нормально распределенная случайная величина с m=24,6 см, и Решение.
Задача № 4 Детали, изготовленные на станке, отличаются по диаметру в силу разных причин. Установлено, что диаметр d – случайная величина, имеющая нормальный закон распределения со стандартом Решение.
Задача № 5 Случайная величина X распределена по нормальному закону с центром рассеяния m. Каким должно быть Решение.
Производная от интеграла с переменным верхним пределом:
Таким образом,
3. Применение нормального закона для изучения случайных величин, распределенных по другим законам.
Задача № 1 Случайная величина – выпадение герба, распределена по биномиальному закону. Биномиальным называется закон, определяющий распределение числа появлений события A, имеющего вероятность p в n независимых опытах. Это число может быть только целым 0, 1, 2,..., k,..., n. Вероятность каждого значения определена зависимостью:
Расчет трудоемок. Доказано, что если При переходе от биномиального к нормальному распределению осуществляется переход от дискретной случайной величины к непрерывной. Для выполнения этого перехода дискретную величину надо ‘’размазать’’ по интервалу. Наиболее рационально выполнить эту операцию приняв в качестве центра интервала значение дискретной величины. Гистограмма распределения непрерывной случайной величины, полученной таким образом, приведена на рисунке.
В результате произведен переход от биномиального распределения непрерывной случайной величины с параметрами: m=25 и В связи с используемым приемом перехода вероятность принятия дискретной величиной значений 20, 21,..., 28 трансформируется в вероятность попадания непрерывной величины на участок 19,5¸28,5.
|

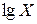 . Тогда вместо X следует рассматривать случайную величину
. Тогда вместо X следует рассматривать случайную величину 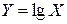 , пересчитав все исходные данные применительно к ней. Получив с помощью формул нормального распределения все необходимые результаты для Y, следует вновь вернуться к исходной случайной величине X.
, пересчитав все исходные данные применительно к ней. Получив с помощью формул нормального распределения все необходимые результаты для Y, следует вновь вернуться к исходной случайной величине X.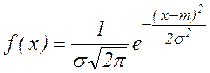 .
.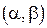 . По определению эта вероятность равна
. По определению эта вероятность равна 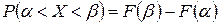 .
.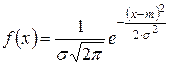 , то
, то 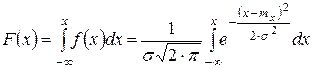 . После известной замены
. После известной замены 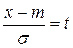 интеграл приводится к виду
интеграл приводится к виду 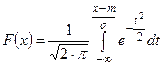 .
.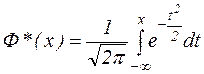 . Функция (*) совпадает с функцией распределения для нормально распределенной случайной величины с параметрами
. Функция (*) совпадает с функцией распределения для нормально распределенной случайной величины с параметрами 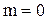 ,
, 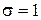 .Функцию распределения
.Функцию распределения 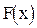 можно выразить через функцию (*)
можно выразить через функцию (*) 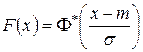 . Интеграл вероятностей имеет вид
. Интеграл вероятностей имеет вид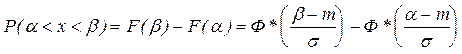 . Аргументы функции
. Аргументы функции 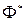 имеют определенный физический смысл: это расстояния от концов интервала до математического ожидания (центра рассеивания), выраженное в средних квадратических отклонениях.
имеют определенный физический смысл: это расстояния от концов интервала до математического ожидания (центра рассеивания), выраженное в средних квадратических отклонениях.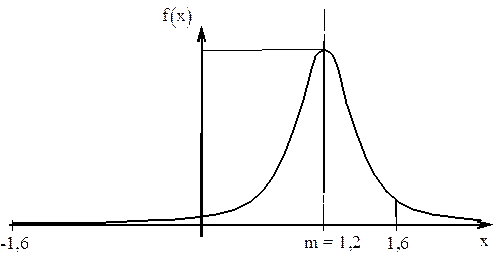
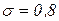 .
.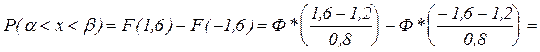
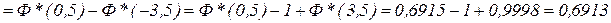 .
.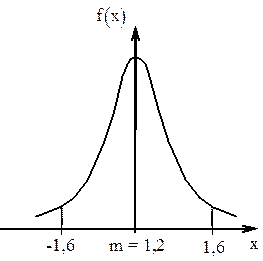
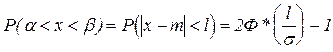
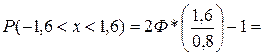
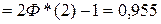 .
.
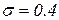 см. Какая часть детали будет иметь длину, выходящую за пределы, заданные техническими условиями.
см. Какая часть детали будет иметь длину, выходящую за пределы, заданные техническими условиями.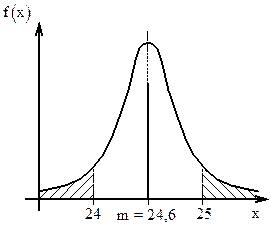
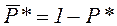 ;
;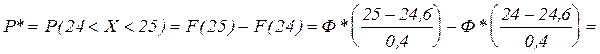
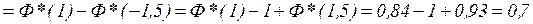 ;
;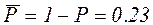 ;
; 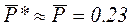 .
.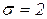 мм. Какова вероятность брака, если им являются детали, диаметр которых отклоняется от нормы более чем на 3,5 мм.
мм. Какова вероятность брака, если им являются детали, диаметр которых отклоняется от нормы более чем на 3,5 мм.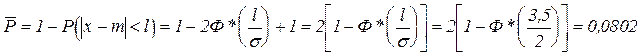 .
.
 для того, чтобы вероятность попадания ее на заданный интервал (
для того, чтобы вероятность попадания ее на заданный интервал (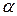 ,
, 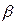 ) достигла максимума.
) достигла максимума.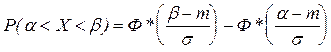 ;
; 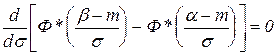 ;
;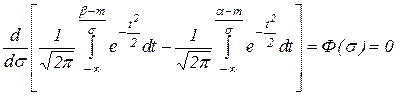 .
.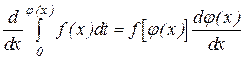
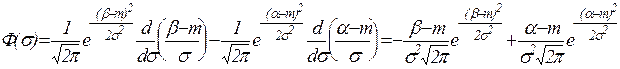 .
.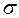 есть корень уравнения:
есть корень уравнения: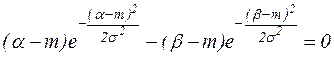 .
.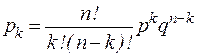 , где
, где 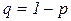 .
.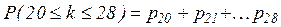
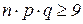 , то биномиальное распределение достаточно точно можно заменить нормальным с параметрами
, то биномиальное распределение достаточно точно можно заменить нормальным с параметрами 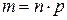 и
и 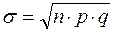 .
.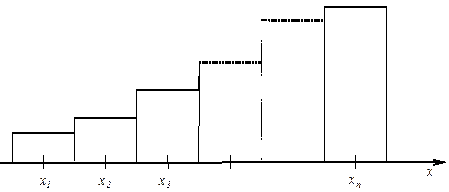
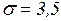 .
.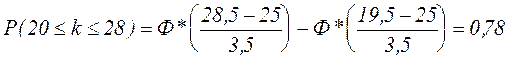 .
.


