Доверительная вероятность
Цель занятия. Изучение понятия квантиля распределения случайной величины. Решение задач с использованием квантилей для определения границ доверительного интервала.
Квантилем
а) Квантиль стандартного нормального закона распределения (m=0 и В этом случае квантиль имеет особое условное обозначение: при Таким образом, если Решение последнего уравнения, полученное с помощью таблицы интеграла вероятности, дает значение x, а вместе с ним и
Если же
Задача № 1. Найти
Определение
б) Квантиль обычного нормального распределения ( В этом случае квантиль имеет обозначение Найдем связь
Задача № 2 Найти Решение.
|

 распределения случайной величины X с функцией распределения
распределения случайной величины X с функцией распределения  называется решение уравнения
называется решение уравнения  . Другими словами квантиль
. Другими словами квантиль  . Вероятность p, задаваемая в %, дает название соответствующему квантилю.
. Вероятность p, задаваемая в %, дает название соответствующему квантилю.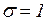 ).
). , а
, а  . Откуда следует, что
. Откуда следует, что  и:
и: ; при
; при  .
. , то
, то  и
и  , где
, где  . В результате
. В результате  . Откуда:
. Откуда:  .
.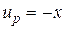 .
.
 , то
, то  и
и  , где
, где  .
. и
и  . Определение
. Определение  . Т.к.
. Т.к.  , то
, то  ,
,  .
.  .
.  .
. .
. . Т.к.
. Т.к.  , то
, то  .
. 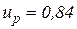 .
. и
и  ).
). .
. ,
,  ,
,  .
. , но
, но  – стандартное распределение и его аргумент есть up, а аргумент исходного распределения x есть
– стандартное распределение и его аргумент есть up, а аргумент исходного распределения x есть  , откуда
, откуда 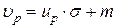 .
. % квантиль нормального распределения при m=1,
% квантиль нормального распределения при m=1, 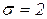

 ; u0,5=0; u0,5=1.
; u0,5=0; u0,5=1.


