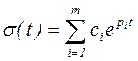Устойчивость автоматических систем

 

Устойчивость АСР является необходимым условием их применения. Пусть система находится в равновесии. Затем она была выведена из этого состояния под действием возмущения. Движение системы под действием возмущения называется вынужденным. Обозначим как x_в(t). В какой-то момент времени эти возмущения были скомпенсированы или устранены. Примем это время за начало отчета (t=0). С этого момента начинается свободное движение системы. Обозначим как x_c(t). Переходный процесс при этом будет являться суммой вынужденных и свободных движений:

h(t) = x_в(t) + x_c(t).

 

АСР устойчива, если при свободном движении она возвращается к исходному или близкому к нему установившемуся (равновесному состоянию). Неустойчивая система не возвращается к состоянию равновесия. Если система совершает около равновесного состояния недопустимо большие колебания, то такая система находится на грани устойчивости.

lim x (t) = 0 - система устойчива;

lim x (t) = const - система нейтральная (или на грани устойчивости);

lim x (t) ® ¥; - система неустойчива.

Наглядно это устойчивость можно продемонстрировать на следующем примере:

устойчивая нейтральная неустойчивая

 

Об устойчивости системы в обобщенном виде можно судить по теореме А.М. Ляпунова. Свободное движение АСР описывается решением ее дифференциального уравнения с правой частью равной 0 (см. полином).

Это уравнение в преобразованном по Лаплассу виде называется характеристическим уравнением АСР:

Решение этого уравнения в общем виде представляет собой сумму экспонент, показатели степени которых равны произведению корней характеристического уравнения на время:

где m - порядок характеристического уравнения

c - постоянные интегрирования;

p - корни характеристического уравнения и отрицательными.

Анализ выражения показывает, что s(t) ® 0 при t ®µ, если p_i < 0

Из этого можно сделать следующие выводы:

1) для устойчивости линейной АСР необходимо и достаточно, чтобы все действительные корни и вещественные части комплексных корней характеристического уравнения были отрицательными;

2) если хотя бы один корней лежит на мнимой оси, то система находится на грани устойчивости;

3) если хотя бы один корней положительный, то система не устойчива.