Типовые динамические звенья
Усилительное (безинерционное) звено. Уравнение связи имеет следующий вид xвых = k xвх,
где k – коэффициент пропорциональности (усиления).
h(t) = k 1(t).
При прохождении сигнала через звено его форма не изменяется, а лишь меняется его величина. Звено не задерживает сигнал, мгновенно пропуская его к выходу. Поэтому звено является безинерционным. В реальных системах таких звеньев нет. Обычно в АСР принимают за такие звенья те, у которых инерционность значительно меньше чем у других. Передаточная функция звена имеет следующий вид W(p) = k.
Статическая и динамическая характеристика усилительного звена совпадают, и поэтому такое звено является статическим. Инерционное звено (апериодическое первого порядка). Уравнение связи имеет следующий вид где T – постоянная времени объекта. При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
Переходный процесс носит не колебательный характер, постоянно (асимптотически) приближаясь к новому равновесному состоянию. Поэтому звено называется инерционным. Чем больше постоянная времени, тем звено более инерционно. Передаточная функция звена имеет следующий вид При t ® ¥ xвых = k xвх..
Следовательно, уравнения статики и динамики совпадают и такое звено является статическим. Колебательное звено (апериодическое второго порядка). Уравнение связи имеет следующий вид
где T1, T2 – постоянные времени объекта. Если T1/T2 < 2, то имеет место колебательное звено. Если T1/T2 ³ 2, то имеет место инерционное звено второго порядка. При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
h(t) = k{1-e-at[coswt + (a/w)sinwt]},
где a = T2/2T12;
где t = 2p/w - период затухания колебаний. x = 2T1/T2 Т.е. при прохождении через звено сигнал, колеблясь относительного нового равновесного состояния с течением времени, затухает, поэтому звено периодическое инерционное. Передаточная функция звена имеет следующий вид При t ® ¥
Уравнение связи будет описываться как xвых = k xвх.. Следовательно, уравнения статики и динамики совпадают и такое звено является статическим. Интегрирующее звено. Уравнение связи имеет следующий вид
Это выражение показывает, что скорость изменения выходного сигнала в данном случае пропорционально величине входного. Уравнение (проинтегрировав) можно записать в следующем виде
Поэтому оно носит название интегрирующего.
h(t) = kt,
При прохождении через звено сигнал монотонно возрастает и не имеет определенного равновесного состояния. Следовательно такое звено является астатическим. Только в случае, когда xвх. = 0, то xвых = const, т.е. при нулевом значении входа выходной сигнал принимает то значение на котором наступило равновесие. Передаточная функция звена имеет следующий вид (Иногда уравнение связи интегрирующего звена записывают в следующем виде
Дифференцирующее идеальное звено. Уравнение связи имеет следующий вид
Данное звено не пропускает сигналы, т.е. и xвых = 0 и только в момент времени t = 0 появления входного воздействия имеет место импульс выходного сигнала. Передаточная функция звена имеет следующий вид Дифференцирующее реальное звено. Уравнение связи имеет следующий вид
Передаточная функция звена имеет следующий вид Следовательно, это звено можно представить как последовательное соединение инерционного звена первого порядка (с передаточной функцией Откуда выражение для общей передаточной функции примет вид
Данное звено не пропускает сигнал. При появлении входного сигнала он поступает на инерционное звено первого порядка и в момент времени t = 0 выходной сигнал возрастает до величины k/T. Далее он поступает на дифференцирующее идеальное звено и поэтому резко асимптотически уменьшается, стремясь к оси абсцисс. Запаздывающее звено. Уравнение связи имеет следующий вид где t – время запаздывания. При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение h(t) =1 (1-t).
Передаточная функция звена имеет следующий вид
Если в передаточной функции заменить комплексную переменную р на jw, то выражение оно будет выглядеть как
Откуда Re(w) = coswt и Im (w)=-sinwt. Тогда
|

 При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
 h(t) = k (1-e-t/T).
h(t) = k (1-e-t/T).
 . Уравнение связи будет описываться как
. Уравнение связи будет описываться как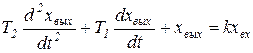

 – частота изменения сигнала
– частота изменения сигнала
 и
и  .
.
 .
. При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
 , где
, где  , и, следовательно, передаточная функция запишется как
, и, следовательно, передаточная функция запишется как  .)
.)
 При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение  .
.

 При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение
При единичном ступенчатом воздействии xвх = 1(t) переходный процесс описывает следующее выражение  .
. .
. ) и дифференцирующего идеального звена с коэффициентом усиления равным 1 (с передаточной функцией
) и дифференцирующего идеального звена с коэффициентом усиления равным 1 (с передаточной функцией  .)
.)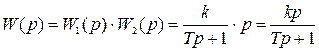 .
.
 При прохождении через звено сигнал не меняет своего значения и формы, только сигнал выхода отстает от входного на отрезок времени t. (Пример - длинный трубопровод.)
При прохождении через звено сигнал не меняет своего значения и формы, только сигнал выхода отстает от входного на отрезок времени t. (Пример - длинный трубопровод.) .
. {по формуле Эйлера} = coswt - jsinwt.
{по формуле Эйлера} = coswt - jsinwt.



