Теория Флори-Хаггинса
Первая термодинамическая теория растворов полимеров была разработана независимо Флори и Хаггинсом в 40-50 гг. XX в. Эта теория сыграла большую роль в понимании физической природы растворов полимеров, многие ее положения используются до настоящего времени. В теории Флори-Хаггинса предполагается, что раствор является регулярным (Регулярный раствор, в отличие от идеального, не является атермическим, но имеет такое же случайное распределение молекул растворенного вещества и растворителя.), а звенья цепей распределены равномерно по всему объему. Это условие не может быть выполнено для очень разбавленных растворов, так как в таком растворе клубки разделены чистым растворителем. Поэтому, строго говоря, теория Флори-Хаггинса применима лишь к умеренно концентрированным или полуразбавленным растворам, для которых характерно заметное перекрывание клубков. Расчет энтропии и энтальпии смешения в теории Флори-Хаггинса проводится на основе модели квазикристаллической решетки, каждая ячейка которой может быть занята либо молекулой растворителя, либо сегментом макромолекулы. В данном случае под сегментом понимается отрезок цепи, объем которого равен объему молекулы растворителя. На рис. 3.2 приведено двухмерное изображение заполненной решетки. Предполагается, что ΔVсм = 0. Общее количество ячеек в решетке равно N1 + σN2, где N1 = n1·NA, N2 = n2·NA; n1, n2 - число молей молекул растворителя и растворенного вещества; σ = Каждая ячейка окружена определенным числом ближайших ячеек. Это число, называемое координационным, обозначается как Z. Оно зависит от типа решетки, однако, на конечные результаты теории влияния не оказывает.
Обозначим через ƒi долю ячеек, заполненных сегментами:
где следует, что число способов размещения (
Множитель 1/2 вводится по той причине, что концы макромолекулы неразличимы, а при изложенном подходе каждая макромолекула помещается в решетку два раза, начиная с одного и другого конца. После завершения расположения макромолекул на оставшиеся места (свободные ячейки) помещаются молекулы растворителя. Однако они не отличаются друг от друга, поэтому имеется лишь один способ их размещения. В итоге общее число возможных вариантов размещения сегментов в растворе, т.е. число микросостояний выразится произведением:
где член 1/N2! введен для того, чтобы учесть перестановки макромолекул между собой, которые не влияют на W. После логарифмирования уравнения (3.31) и ряда преобразований (Тенфорд Ч. Физическая химия полимеров. М: Химия, 1965.), включающих использование формулы Стирлинга и уравнения (3.26), получаем:
Поскольку в рассматриваемой модели предполагается равенство объемов, занимаемых молекулой растворителя и сегмента макромолекулы, то:
где φ1, φ2 - объемные доли растворителя и растворенного полимера. С учетом этого уравнение (3.32) приобретает следующий вид:
На основе решеточной модели раствора была также рассчитана энтальпия смешения ΔHсм. Обозначим e11, e22, е12 энергию одного контакта, т.е. энергию, необходимую для разделения двух молекул растворителя, двух сегментов макромолекул и молекулы растворителя с сегментом полимера. Каждая молекула растворителя имеет в своем непосредственном окружении (координационной сфере) из Z ячеек
То же самое можно сказать о сегментах макромолекул, но, поскольку их контакты с растворителем учтены выше, отметим лишь то, что каждый сегмент контактирует с
С учетом обозначенных выше контактов энтальпия смешения n1 моль и n2 моль растворенного вещества (полимера) будет описываться следующим выражением:
Это выражение можно переписать в более простой форме:
где ΔЕ - энергия взаимообмена, в данном случае равная:
Поскольку число Z не может быть определено в рамках теории Флори-Хаггинса, вводится полуэмпирический параметр
где Δе и ΔЕ - молекулярная и молярная энергии взаимообмена. Из (3.38) следует, что
Используя выражение для ΔSсм (3.34) и для ΔSсм (3.39), легко может быть получено выражение для функции Гиббса смешения:
Выражение, описывающее изменение химического потенциала растворителя в растворе полимера, Флори и Хаггинс получили через парциальную энтальпию и энтропию смешения
Конечный результат имеет вид:
Выражения для активности компонентов получены Хаггинсом. Ниже приводится одно из них, описывающее активность растворителя в растворе полимера:
Уравнения (3.40), (3.42), (3.43) наиболее значимы в рассматриваемой теории. Знак ΔGсм определяет принципиальную возможность растворения, а значения Δµ1 и In a1 определяют экспериментально изучаемые свойства растворов полимеров - осмотическое давление и упругость пара растворителя над раствором. Теория Флори - Хаггинса, несмотря на недостатки, некоторые из которых будут отражены ниже, по праву считается классической, а параметр взаимодействия В модели Флори-Хаггинса предполагалось, что заполнение любой ячейки решетки равновероятно для молекулы или сегмента. Такое допущение справедливо лишь при ΔЕ ≈ 0. Если ΔE ≠ 0, то некоторые из контактов являются более предпочтительными, а это означает, что энтропия смешения не равна в точности конфигурационной энтропии. Эти соображения привели к необходимости корректировки теории, которая была проведена Флори и Киргбаумом путем введения некоторых дополнительных параметров. Было предположено, в частности, что параметр взаимодействия
Рассмотрим происхождение второго параметра. В первоначальной теории для парциальной энтропии растворителя получено:
Разложив ln(1 - φ2) в ряд и ограничившись двумя его первыми членами, получаем:
При большом числе а вторым членом уравнения можно пренебречь, следовательно:
Поскольку оказалось, что парциальная энтропия смешения зависит от природы растворителя, авторы ввели множитель Ψ1, чтобы учесть это явление. В результате было получено уравнение (3.45), приведенное выше. Если в первоначальном варианте теории энергия взаимообмена Δе была выражена через параметр Таблица 3.2 Параметр термодинамического взаимодействия
Киргбаум связали Δе с параметрами Ψ1, K1 и θ-температурой следующим образом:
Связь между упомянутыми выше параметрами дается соотношением:
|

 - число сегментов цепи.
- число сегментов цепи.
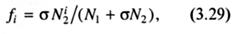
 - i молекул N2. Рассмотрим число возможных способов размещения (
- i молекул N2. Рассмотрим число возможных способов размещения (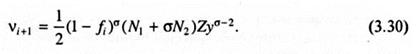








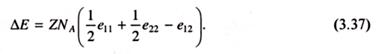
 , называемый параметром взаимодействия Флори-Хаггинса. Согласно определению:
, называемый параметром взаимодействия Флори-Хаггинса. Согласно определению:
 1 численно равен энергии, необходимой для переноса одной молекулы или одного моля растворителя из чистого растворителя в полимер, отнесенной к «тепловой» энергии kТипи RT. С учетом (3.38)
1 численно равен энергии, необходимой для переноса одной молекулы или одного моля растворителя из чистого растворителя в полимер, отнесенной к «тепловой» энергии kТипи RT. С учетом (3.38)

 и
и 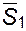 поскольку
поскольку


 1 от концентрации раствора и молекулярной массы полимера, хотя теория не предусматривает ни того, ни другого. Существует несколько вариантов «улучшенной» теории. Один из них разработан Флори и Киргбаумом для разбавленных растворов полимеров.
1 от концентрации раствора и молекулярной массы полимера, хотя теория не предусматривает ни того, ни другого. Существует несколько вариантов «улучшенной» теории. Один из них разработан Флори и Киргбаумом для разбавленных растворов полимеров. имеет две составляющие - энергетическую и энтропийную, обозначенные как κ1 и Ψ1. Их физический смысл определяется уравнениями:
имеет две составляющие - энергетическую и энтропийную, обозначенные как κ1 и Ψ1. Их физический смысл определяется уравнениями:



 1 то в усовершенствованном варианте Флори и
1 то в усовершенствованном варианте Флори и




