Коллигативные свойства растворов полимеров. Осмотическое давление
К коллигативным свойствам относятся: снижение давления пара растворителя в растворе по сравнению с чистым растворителем; понижение температуры замерзания раствора по сравнению с температурой замерзания растворителя; повышение температуры кипения раствора по сравнению с температурой кипения растворителя; осмотическое давление. Общее определение коллигативных свойств состоит в том, что они являются количественной мерой химического потенциала растворителя в растворе. Другое определение коллигативных свойств состоит в том, что они являются количественной мерой числа частиц растворенного вещества. Под частицами в данном случае понимаются молекулы, коллоидные частицы, макромолекулы. Для того, чтобы убедиться в справедливости такого определения, преобразуем уравнение (3.9). Для очень разбавленных растворов полимеров, когда Х2 → 0, можно записать:
что приводит к
Выразим концентрацию растворенного вещества через молярную концентрацию. В рассматриваемом случае (Х2 → 0) объем раствора практически равен n1
где с2, С2 - массовая и молярная концентрации; М2 - молекулярная масса растворенного вещества. С учетом рассмотренного, уравнение (3.52) может быть записано следующим образом:
Из уравнения (3.54) следует, что Δµ1 растворителя и, следовательно, значения коллигативных свойств растворов определяются числом частиц (с2/М2) растворенного вещества. Коллигативные свойства обычно используются для определения молекулярной массы растворенных веществ. Значения этих свойств малы для растворов полимеров по сравнению с растворами низкомолекулярных соединений с одинаковыми массовыми концентрациями растворенного вещества. Однако значения осмотического давления разбавленных растворов (порядка 10 мм рт. ст.) вполне пригодны для измерения. Поэтому данный метод широко используется для нахождения среднечисловой молекулярной массы полимеров и термодинамической характеристики их растворов. Осмотическое давление возникает вследствие самопроизвольной диффузии растворителя из раствора меньшей концентрации (или растворителя) в раствор большей концентрации через полупроницаемую перегородку (рис. 3.3). Избыточное гидростатическое давление, возникающее в той области, куда переносится растворитель, препятствует его диффузии, в результате чего в течение определенного времени устанавливается равновесие. Величина осмотического давления принимается равной гидростатическому давлению столба жидкости в капилляре, погруженном в жидкость той камеры осмометра (прибор для измерения), в которую направлен диффузионный поток растворителя (рис. 3.3).
При установлении равновесия химический потенциал растворителя по обе стороны мембраны, т.е. в растворе и растворителе, должен быть одинаков. Следовательно, осмотическое давление можно определить как давление, которое следует приложить к раствору с тем, чтобы увеличить химический потенциал растворителя в нем до величины, характерной для чистого растворителя, т.е.
Поскольку
В пределе, для очень разбавленных растворов, близких по свойствам к идеальным, используя (3.54) и ограничиваясь первым членом ряда в скобках, можно получить уравнение Вант-Гоффа:
Среднечисловая молекулярная масса полимеров. Уравнение (3.57) необходимо скорректировать с учетом полидисперсности полимера. Рассмотрим пример, содержащий n1, n2, n3,... моль макромолекул с молекулярными массами М1, М2, М3,... Суммарные массы макромолекул с одинаковой молекулярной массой в этом случае будут равны с1 = n1М1, с2 = n2М2, с3 = n3М3..., а суммарная масса полимера с = с1 + с2 + с3 +... = Уравнение (3.57) можно записать в виде:
где n - число молей растворенного вещества, тогда для раствора полидисперсного полимера
Разделив уравнение (3.59) на с =
|



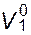 , где n1, - число молей растворителя, а
, где n1, - число молей растворителя, а  , где
, где 


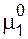 =
=  :
: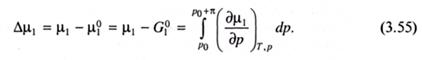
 µ1/,
µ1/,  p =
p = 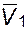 и последняя величина практически не зависит от давления,то:
и последняя величина практически не зависит от давления,то:

 .
.

 и учитывая, что, согласно определению, среднечисловая молекулярная масса полимера равна
и учитывая, что, согласно определению, среднечисловая молекулярная масса полимера равна 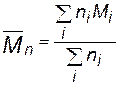 , окончательно получаем:
, окончательно получаем:



