Ограниченная растворимость. Фракционирование
Для растворов высокомолекулярных соединений, как и для смесей низкомолекулярных веществ, характерно явление ограниченной растворимости. При достижении предельной растворимости полимеров в результате изменения температуры или концентрации раствор разделяется на две фазы. Здесь возможны два случая. Если полимер способен кристаллизоваться, то при определенных условиях выделяется твердая кристаллическая фаза. Растворы аморфных полимеров разделяются на две жидкие фазы - разбавленный и концентрированный растворы полимера. Такое разделение называется жидкостным. На рис. 3.6 приведены типичные фазовые диаграммы состояния растворов полимеров в координатах температура - состав. Кривые, называемые бинодалью, разделяют каждую из диаграмм на две области. Область внутри бинодали соответствует двухфазному раствору. При определенных температурах ветви бинодали сходятся. Такие температуры называются критическими, в этих точках составы соответствующих фаз равны. Максимум бинодали отвечает верхней критической температуре смешения (ВКТС), а минимум - нижней (НКТС).
Выше было показано, что в зависимости от температуры растворитель может быть плохим, идеальным и хорошим для одного и того же полимера. Ясно, например, что, в окрестности ВКТС, когда полимер выделяется из раствора, растворитель является плохим, A2 < 0. Последнее условие не может реализоваться в достаточно широком температурном интервале, поэтому θ-температура (А2 = 0) должна быть достаточно близка к ВКТС. Для растворов полимеров НКТС и ВКТС наблюдаются для одной системы, как и для смесей низкомолекулярных жидкостей. Однако если в последнем случае ВКТС > НКТС и диаграмма состояния раствора является замкнутой фигурой, близкой к овалу, то для растворов полимеров часто характерно НКТС > ВКТС, что приводит к необычному виду диаграммы (рис. 3.6). Обычно НКТС реализуются при высоких температурах (табл. 3.3), как правило, превышающих температуру кипения растворителя, вследствие чего система оказывается под значительным давлением. Для систем с ВКТС и НКТС существуют две θ-температуры; та, что соответствует ВКТС, называется θ-температурой Флори, вторая - θ-температурой Роулинса. Последняя обычно близка к критической температуре растворителя. Термодинамическим условием существования ВКТС и НКТС является соответственно ΔН > О, ΔS > 0 и ΔН < О, ΔS < 0. Теория Флори-Хаггинса рассматривает системы с ΔН ≥ 0, поэтому эта теория может предсказать существование лишь ВКТС. Согласно теории, положение точки ВКТС (φ2к) определяется выражением:
Таблица 3.3 Критические температуры смешения и θ -температуры для некоторых растворов полимеров, °С
Поскольку парциальный мольный объем полимера
При М2 → ∞ Из рис. 3.6 видно, что растворимость полимера зависит от его молекулярной массы. Это обстоятельство широко используется на практике для фракционирования - разделения полидисперсного полимера по молекулярным массам. Теория фракционирования разработана Бренстедом и Шульцем. Выше упоминалось, что при жидкостном разделении раствора полимера образуются две фазы - разбавленная и концентрированная. Согласно теории фракционирования,
где
где На практике фракционирование из раствора проводят, уменьшая термодинамическое качество растворителя, путем изменения температуры или добавлением осадителя. При этом последовательно выделяются фракции полимера в порядке уменьшения их средней молекулярной массы. Последнее нужно подчеркнуть особо, так как выделяющиеся фракции не являются монодисперсными.
|



 пропорционален его молекулярной массе и по этой причине намного больше парциального мольного объема растворителя
пропорционален его молекулярной массе и по этой причине намного больше парциального мольного объема растворителя 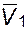 при М2 → ∞
при М2 → ∞  → ∞ и φ2к → 0. Отсюда следует, что точка ВКТС наблюдается при малом содержании полимера, и следовательно, диаграммы фазового состояния растворов полимеров смещены в область малых концентраций по сравнению с аналогичными диаграммами для растворов низкомолекулярных веществ. Второй вывод относится к термодинамической характеристике раствора в точке ВКТС. Величина параметра взаимодействия в этой точке описывается выражением:
→ ∞ и φ2к → 0. Отсюда следует, что точка ВКТС наблюдается при малом содержании полимера, и следовательно, диаграммы фазового состояния растворов полимеров смещены в область малых концентраций по сравнению с аналогичными диаграммами для растворов низкомолекулярных веществ. Второй вывод относится к термодинамической характеристике раствора в точке ВКТС. Величина параметра взаимодействия в этой точке описывается выражением: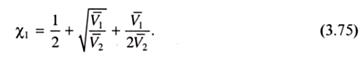
 → 0 и
→ 0 и  1 → 1/2, следовательно, ВКТС может рассматриваться как 0-температура раствора полимера с бесконечно большой молекулярной массой, и в этих условиях растворитель можно охарактеризовать как идеальный.
1 → 1/2, следовательно, ВКТС может рассматриваться как 0-температура раствора полимера с бесконечно большой молекулярной массой, и в этих условиях растворитель можно охарактеризовать как идеальный.
 ,
,  - объемные доли полимера в концентрированной и разбавленной фазах, х - параметр, пропорциональный молекулярной массе полимера. В том случае, когда молекулярные массы звена полимера и растворителя совпадают, х = р = М/М0, где p - число звеньев в цепи, М и М0 - молекулярные массы полимера и мономерного звена. Величина параметра а связана с термодинамическим качеством растворителя, из которого выделяется полимер, следующим образом:
- объемные доли полимера в концентрированной и разбавленной фазах, х - параметр, пропорциональный молекулярной массе полимера. В том случае, когда молекулярные массы звена полимера и растворителя совпадают, х = р = М/М0, где p - число звеньев в цепи, М и М0 - молекулярные массы полимера и мономерного звена. Величина параметра а связана с термодинамическим качеством растворителя, из которого выделяется полимер, следующим образом:



