Исключенный объем и термодинамические свойства раствора
Вернемся вновь к проблеме исключенного объема (2.1.2) с тем, чтобы выявить влияние на него параметров, характеризующих термодинамическое качество растворителя. Исключенный объем макромолекулы (3iV/ определяется исключенным объемом сегмента β (Имеется в виду термодинамический сегмент Куна.):
где n* - число сегментов*. Эффективный исключенный объем сегмента β* учитывает вероятность того, что в элементарном объеме, занятом одним сегментом, не может находиться другой сегмент. Он определяется соотношением:
где r - расстояние между взаимодействующими сегментами; U(r) - потенциальная энергия взаимодействия двух сегментов в растворе. Эффективный исключенный объем сегмента определяется балансом сил притяжения и отталкивания. Из рассмотренного ранее ясно, что при θ-условиях β* = 0, в хороших растворителях β* > 0. В теории Флори-Хаггинса влияние исключенного объема учитывается параметром z, который для гауссова клубка описывается соотношением:
где l* - длина сегмента Куна. Из (3.71) следует, что параметр z пропорционален исключенному объему сегмента и обратно пропорционален объему макромолекулы. Последнее указывает на то, что параметр z зависит от частоты столкновений сегментов в макромолекулярном клубке.
Решеточная модель Флори-Хаггинса позволяет рассчитать величину параметра z теоретически. Было получено следующее выражение:
где Связь параметра z с коэффициентом набухания клубка а была отмечена нами ранее (2.25). Более строгие по сравнению с теорией Флори-Хаггинса расчеты показывают, что числовой коэффициент в этом уравнении должен быть несколько изменен. Таким образом, имеем окончательно:
|



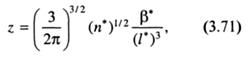
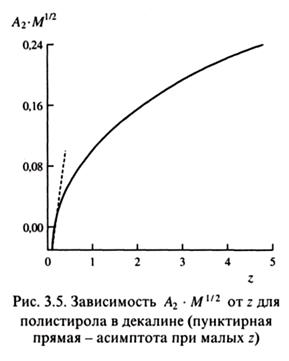

 - парциальный удельный объем полимера. Параметр z связан определенным образом со вторым вириальным коэффициентом А2. Типичная для растворов полимеров зависимость приведена на рис. 3.5.
- парциальный удельный объем полимера. Параметр z связан определенным образом со вторым вириальным коэффициентом А2. Типичная для растворов полимеров зависимость приведена на рис. 3.5.



