Корневой критерий.Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость. Корни характеристического уравнения могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости.
Виды корней характеристического уравнения:
положительные (корень № 1); отрицательные (2); нулевые (3); - Комплексные комплексные сопряженные (4); чисто мнимые (5); По кратности корни бывают: одиночные (1, 2, 3); сопряженные (4, 5): si = a ± jw; кратные (6) si = si+1 = … Корневой критерий формулируется следующим образом: Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива. Пример 3.1. Передаточная функция системы имеет вид: Характеристическое уравнение: s3 + 2s2 + 2.25s + 1.25 = 0. Корни: s1 = -1; s2 = -0,5 + j; s3 = -0,5 - j. Следовательно, система устойчива. ¨ Границей устойчивости является мнимая ось Im.
|
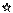(Символом обозначены корни уравнения).
- Действительные:
.
