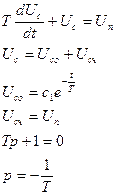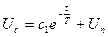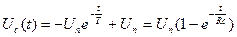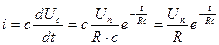Разработка математической дискретной модели объекта.
Математическая модель объекта или системы управления – это совокупность математических уравнений отражающих взаимосвязь выходных и входных величин, дополненная ограничениями, накладываемыми на эти величины условиями их физической реализации и эксплуатации. Математическая модель может как вскрывать, так и не вскрывать сущность протекающих в объекте процессов или явлений. Полная математическая модель включает в себя статическую и динамическую. Статическая модель – это описание связей между входами и выходами в установившемся равновесном состоянии без учета времени. Динамическая модель – это описание связей между входами и выходами в переходном процессе, неустановившемся режиме с учетом времени, т.е. когда объект переходит из одного установившегося состояния в другое. Различают два вида математических моделей: · детерминированная · стохастическая Детерминированные модели позволяют однозначно рассчитать значение выхода при известном входе. Стохастические модели – это модели, в которых отсутствует четкое соответствие между значениями входов и выходов, взаимосвязь между ними описывается случайными функциями времени, определяющими вероятность того или иного значения выхода при известном значении входа в данный момент входа. При построении математических моделей используется два подхода: · детерминированный подход · экспериментально-статистический подход Детерминированный подход заключается в составлении математического описания объекта, при котором находят уравнение статики и динамики на основе теоретического анализа физических и химических процессов, протекающих в исследуемом объекте. При выводе уравнений используются фундаментальные законы сохранения вещества и энергии, а также различные кинетические закономерности, законы переноса тепла и массы и т.д. Достоинства подхода является наименьшая затратность математических и энергетических ресурсов. Недостаток заключается в том, что этот подход сопряжен с трудностью решения и анализа составляемых уравнений и требует проведения специальных исследований для определения численных значений коэффициентов полученных уравнений. Рассмотрим пример использования детерминированного подхода при моделировании и исследовании электрической RC-цепочки, при подаче на ее вход постоянного напряжения.
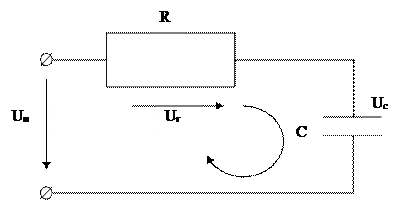
Используя: 1. II закон Кирхгоффа; 2. закон Ома; 3. закон изменения величины тока в конденсаторе,- промоделируем работу RC-цепочки.
Обозначим
Общее решение дифференциального уравнения I порядка будет иметь вид:
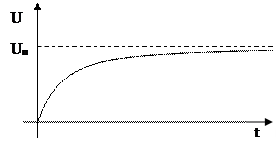
Начальные условия: Частное решение:
Второй подход состоит в определении характеристик реального объекта путем постановки на нем специального эксперимента. Метод прост, обладает малой трудоемкостью, позволяет точно определить свойства объекта. Вместе с тем, он требует оснащения изучаемого объекта специальным экспериментальным оборудованием и проведение специальных исследований, т.е. является более затратным в материальном плане.
|

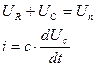
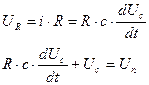
 равным Т, тогда
равным Т, тогда