Идентификация объекта регулирования с использованием векторно-матричного описания
Конечно-разностное уравнений может быть представлено в векторно-матричном виде следующим образом:
где
Критерий метода наименьших квадратов в векторно-матричном виде запишется:
Вектор экспериментальных значений выхода размерности n0 примет вид:
С учетом выражения (1.1) вектор y может быть представлен следующим выражением:
где = Это матрица экспериментальных значений входа и выхода. Каждая из строк которой предназначена для расчета по модели соответствующего выхода объекта. С учетом выражения (1.3) критерий метода наименьших квадратов примет следующий вид:
Система линейных уравнений, полученная путем дифференцирования критерия Ф по параметрам конечно-разностного уравнения примет вид:
где Выполняя преобразование выражений (1.5.а) и (1.5.b) можно представить их в виде:
Выражая из (1.6.а) и (1.6.б) вектор параметров конечно-разностных уравнений получим:
Как видно из формул расчета вектор оценок искомых параметров модели (1.7.а), (1.7.б) необходимым условием является обратимость матрицы Если количество измерений N0 меньше количества искомых параметров (n+1), то ранг матрицы
|
(1.1)
, где 
(1.2).
. Вектор, рассчитанных по модели значений выхода объекта, размерностью n0 :
(1.3)
матрица вида
(1.4)
(1.5.а)
или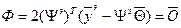 
(1.5.b)
(1.6.а)
(1.6.b)
. Из вида матрицы 
, имеющей размерность 
следует, что ее ранг не может превышать наименьшую размерность, т.е. 
, тогда по известному свойству ранг произведения 
. На основе этого равенства следует, что определитель матрицы 
, поскольку размерность 
. В этом случае система уравнений (1.5.а), (1.5.b) может быть либо несовместимой (т.е. не имеет решения), либо не определенной (имеет бесконечное множество решений). Вне зависимости от результата из полученного следует, что оценка параметров конечно-разностного уравнения не может быть найдена. Таким образом, при идентификации экспериментальных значений должно быть больше количества определяемых параметров КРУ.
