Получение конечно-разностных уравнений цифровых регуляторов и области допустимых изменений параметров.
Цифровой регулятор в общем виде может быть представлен конечно-разностным уравнением m-го порядка. Структурная схема регулятора:
где
Ошибка регулирования определяется следующим выражением: где
Подставляя правую часть в уравнение регулятора получим: Получим конечно-разностное уравнение цифрового регулятора из дифференциального уравнения ПИД-регулятора: где
Продифференцируем обе части уравнения, получим:
Заменим производные конечно-разностным уравнением, получим:
Понизим индекс на единицу:
Полученное уравнение называется конечно-разностным уравнением цифрового регулятора второго порядка, где 1. параметры цифрового регулятора можно вычислить по настройкам, что позволяет реализовать аналоговый регулятор с помощью цифровой вычислительной техники 2. из уравнения взаимосвязи настроек цифрового и аналогового регуляторов видно, что они равны по количеству, т.е. настройка цифрового равна настройке аналогового регулятора 3. из уравнения взаимосвязи видно, что размерность настроек цифрового регулятора совпадает с размерностью настроек аналогового регулятора Для получения конечно-разностного уравнения ПИ регулятора необходимо постоянную дифференцирования приравнять к нулю. Дифференциальное уравнение ПИ-регулятора:
Цифровые настройки будут равны: Следовательно цифровой ПИ-регулятор примет вид: 1. 2. 3.
Расчет переходного процесса по конечно-разностным уравнениям должен выполнятся на основе начальных условий, которые примут вид:
Построим переходной процесс для ПИД-закона в цифровом виде. Для этого запишем ограничения на настройки цифрового регулятора, обеспечивающие реализацию ПИД закона. При этом 1. 2. 3. 4. 5. 6. 7.
Для расчета переходного процесса цифрового ПИД-регулятора зададим начальные условия:
Цифровой регулятор, описывающийся конечно-разностным уравнением, охватывает больший класс законов регулирования, чем аналоговый. При выполнении ограничений на настройки цифрового регулятора они реализуют аналоговые законы. В противном случае – чисто цифровые законы регулирования. Внимание! При выводе конечно-разностных уравнений цифровых регуляторов дифференцируют обе части уравнений аналогового регулятора только в том случае, когда есть интегрирующая составляющая. Для регулятора, описываемого конечно-разностным уравнением m-го порядка, в общем случае
|


 ,
,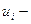 выход регулятора (регулирующее воздействие),
выход регулятора (регулирующее воздействие),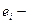 ошибка регулирования сигнала рассогласования,
ошибка регулирования сигнала рассогласования, настроечные параметры цифрового регулятора,
настроечные параметры цифрового регулятора,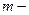 порядок цифрового регулятора.
порядок цифрового регулятора. ,
,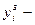 задающее воздействие,
задающее воздействие,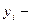 текущее значение регулируемой величины.
текущее значение регулируемой величины. .
.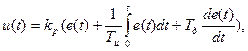
 коэффициент усиления,
коэффициент усиления,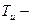 время изодрома,
время изодрома,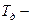 время предварения.
время предварения.
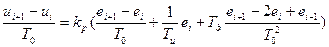 . Выразим
. Выразим :
:  .
.





 настроечные параметры. Полученное уравнение позволяет выполнить следующее:
настроечные параметры. Полученное уравнение позволяет выполнить следующее:
 ,
,  ,
, 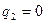
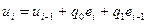 . Построим график переходного процесса для регулятора первого порядка (цифровой ПИ-регулятор) при подаче на его вход единичного ступенчатого воздействия. Для этого укажем ограничения для
. Построим график переходного процесса для регулятора первого порядка (цифровой ПИ-регулятор) при подаче на его вход единичного ступенчатого воздействия. Для этого укажем ограничения для  , необходимые для реализации ПИ-закона в цифровом виде:
, необходимые для реализации ПИ-закона в цифровом виде: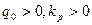 или
или 
 или
или 
 для ПИ-регулятора
для ПИ-регулятора при условии, что
при условии, что 

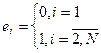
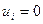
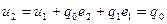


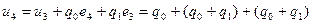


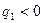
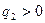



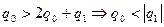



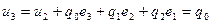
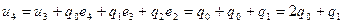



 . Начальные условия для расчета переходного процесса будут иметь вид:
. Начальные условия для расчета переходного процесса будут иметь вид: 





