Одним из способов оценки качества работы системы регулирования является определение ее реакции на типовое входное воздействие по заданию или по возмущению. При этом рассчитываются такие показатели качества переходного процесса как:
- интегрально-квадратичная ошибка,
- время регулирования,
- статическая ошибка,
- динамическая ошибка,
- коэффициент затухания,
кроме того, по виду переходного процесса можно судить об устойчивости и запасе устойчивости системы. Для расчета оптимизации цифрового регулятора необходимо задать исходные данные:
- критерий оптимизации
- динамическая модель объекта
- уравнение регулятора с заданной структурой и неизвестными, оптимизируемыми коэффициентами
Наиболее общим критерием качества регулирования является интегрально-квадратичная ошибка 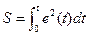 . Задача оптимизации заключается в определении таких значений настроек
. Задача оптимизации заключается в определении таких значений настроек  , которые обеспечивают минимум выбранного критерия. Рассмотрим алгоритм оптимизации на примере цифрового регулятора n-го порядка и объекта регулирования порядка m с запаздыванием:
, которые обеспечивают минимум выбранного критерия. Рассмотрим алгоритм оптимизации на примере цифрового регулятора n-го порядка и объекта регулирования порядка m с запаздыванием:
 (1)
(1)
В дискретном виде интегрально-квадратичная ошибка рассчитывается по формуле:
 (2)
(2)
где  вектор настроечных параметров цифрового регулятора.
вектор настроечных параметров цифрового регулятора.
Необходимым и достаточным условием существования минимального критерия S является равенство нулю (первых частных производных критерия по настроечным параметрам регулятора), т.е.
 (3)
(3)
Полученная система (3) может быть описана одним уравнением вида:
 т.к. из системы уравнений (3) нельзя получить аналитическое выражение с известными коэффициентами относительно параметров вектора q (аналогично критерию метода наименьших квадратов), то воспользуемся одним из численных методов оптимизации, например методом градиента с пошаговым поиском оптимальных настроек. Поиск оптимума критерия (2) проводится в два этапа:
т.к. из системы уравнений (3) нельзя получить аналитическое выражение с известными коэффициентами относительно параметров вектора q (аналогично критерию метода наименьших квадратов), то воспользуемся одним из численных методов оптимизации, например методом градиента с пошаговым поиском оптимальных настроек. Поиск оптимума критерия (2) проводится в два этапа:
- находятся числовые значения частных производных критерия по каждой из настроек. (система уравнений (3)), которая определяет направление градиента в исходной точке или на каждой итерации приближений.
- осуществляется шаг по каждой из настроек вектора q в направлении убывания целевой функции (2) по следующей формуле:
 (4)
(4)
Полученную систему уравнений (4) можно описать общим уравнением вида:

где  номер текущей итерации в приближении к оптимуму
номер текущей итерации в приближении к оптимуму
 коэффициент шага для k-ой настройки на l-ой итерации
коэффициент шага для k-ой настройки на l-ой итерации
 норма градиента на l-ой итерации
норма градиента на l-ой итерации
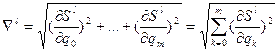 (5)
(5)
При выполнении шага одновременно изменяются значения всех настроек 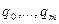 причем каждая из них передается приращение пропорциональности соответствующей координате градиента соответствующей частной производной
причем каждая из них передается приращение пропорциональности соответствующей координате градиента соответствующей частной производной  . Стратегия изменения шага
. Стратегия изменения шага  зависит от того, сменился ли знак производной по соответствующей настройке на последней итерации или нет.
зависит от того, сменился ли знак производной по соответствующей настройке на последней итерации или нет.
 (6)
(6)
Такая стратегия изменения шага  обеспечивает наибольшую скорость сходимости в далее от экстремума критерия и достаточно быстрое достижение оптимума в его окрестности за счет уменьшения коэффициента шага при изменении знака производной. В момент окончания поиска оптимума определяется при выполнении заранее заданных условий, которые имеют вид:
обеспечивает наибольшую скорость сходимости в далее от экстремума критерия и достаточно быстрое достижение оптимума в его окрестности за счет уменьшения коэффициента шага при изменении знака производной. В момент окончания поиска оптимума определяется при выполнении заранее заданных условий, которые имеют вид:  или
или  (7)
(7)
где  определяет точность вычисления точки экстремума. Для вычисления нового приближения по формулам (4) надо предварительно рассчитать численные значения частных производных критерия по формулам (3) для этого необходимо провести расчет переходного процесса замкнутой ЦСР по уравнениям (1) при подаче единичного ступенчатого воздействия на вход системы для этого необходимо знать параметры ОР
определяет точность вычисления точки экстремума. Для вычисления нового приближения по формулам (4) надо предварительно рассчитать численные значения частных производных критерия по формулам (3) для этого необходимо провести расчет переходного процесса замкнутой ЦСР по уравнениям (1) при подаче единичного ступенчатого воздействия на вход системы для этого необходимо знать параметры ОР  и выбрать в качестве первого приближения настройки регулятора
и выбрать в качестве первого приближения настройки регулятора  исходя из физической реализации того или иного регулятора. Рассчитаем переходной процесс в результате которого полученное значение выхода регулятора
исходя из физической реализации того или иного регулятора. Рассчитаем переходной процесс в результате которого полученное значение выхода регулятора  и выхода ОР
и выхода ОР  . Затем проводится расчет численных значений частных производных выхода регулятора и объекта по оптимизируемым настройкам
. Затем проводится расчет численных значений частных производных выхода регулятора и объекта по оптимизируемым настройкам

с помощью квазианалитических рекуррентных зависимостей, которые получаются путем взятия производных от уравнения регулятора и объекта по оптимизируемым настройкам.
Берем уравнение регулятора и дифференцируем: 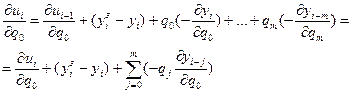
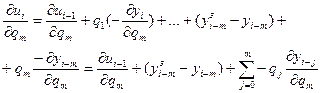


Используя сокращенную запись, данную систему уравнений можно представить в виде:
 (8)
(8)
Для расчета переходного процесса по системе уравнений (2) и численных значений частных производных системы уравнений (8) необходимо задать начальные условия

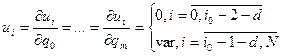

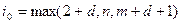
Замечание 1: расчет численных значений частных производных осуществляется по формуле (8) аналогично расчету переходного процесса по заданию.
Замечание2: коэффициент шага  на первой итерации приближения не может быть рассчитан по правилу (6), в качестве его начальных значений можно принять:
на первой итерации приближения не может быть рассчитан по правилу (6), в качестве его начальных значений можно принять:

Замечание 3: частные производные выходов регулятора и объекта по одной и той же настройке должны рассчитываться в одном и том же цикле.

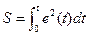 . Задача оптимизации заключается в определении таких значений настроек
. Задача оптимизации заключается в определении таких значений настроек  , которые обеспечивают минимум выбранного критерия. Рассмотрим алгоритм оптимизации на примере цифрового регулятора n-го порядка и объекта регулирования порядка m с запаздыванием:
, которые обеспечивают минимум выбранного критерия. Рассмотрим алгоритм оптимизации на примере цифрового регулятора n-го порядка и объекта регулирования порядка m с запаздыванием: (1)
(1) (2)
(2) вектор настроечных параметров цифрового регулятора.
вектор настроечных параметров цифрового регулятора. (3)
(3) т.к. из системы уравнений (3) нельзя получить аналитическое выражение с известными коэффициентами относительно параметров вектора q (аналогично критерию метода наименьших квадратов), то воспользуемся одним из численных методов оптимизации, например методом градиента с пошаговым поиском оптимальных настроек. Поиск оптимума критерия (2) проводится в два этапа:
т.к. из системы уравнений (3) нельзя получить аналитическое выражение с известными коэффициентами относительно параметров вектора q (аналогично критерию метода наименьших квадратов), то воспользуемся одним из численных методов оптимизации, например методом градиента с пошаговым поиском оптимальных настроек. Поиск оптимума критерия (2) проводится в два этапа: (4)
(4)
 номер текущей итерации в приближении к оптимуму
номер текущей итерации в приближении к оптимуму коэффициент шага для k-ой настройки на l-ой итерации
коэффициент шага для k-ой настройки на l-ой итерации норма градиента на l-ой итерации
норма градиента на l-ой итерации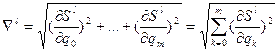 (5)
(5)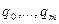 причем каждая из них передается приращение пропорциональности соответствующей координате градиента соответствующей частной производной
причем каждая из них передается приращение пропорциональности соответствующей координате градиента соответствующей частной производной  . Стратегия изменения шага
. Стратегия изменения шага  зависит от того, сменился ли знак производной по соответствующей настройке на последней итерации или нет.
зависит от того, сменился ли знак производной по соответствующей настройке на последней итерации или нет. (6)
(6) или
или  (7)
(7) определяет точность вычисления точки экстремума. Для вычисления нового приближения по формулам (4) надо предварительно рассчитать численные значения частных производных критерия по формулам (3) для этого необходимо провести расчет переходного процесса замкнутой ЦСР по уравнениям (1) при подаче единичного ступенчатого воздействия на вход системы для этого необходимо знать параметры ОР
определяет точность вычисления точки экстремума. Для вычисления нового приближения по формулам (4) надо предварительно рассчитать численные значения частных производных критерия по формулам (3) для этого необходимо провести расчет переходного процесса замкнутой ЦСР по уравнениям (1) при подаче единичного ступенчатого воздействия на вход системы для этого необходимо знать параметры ОР  и выбрать в качестве первого приближения настройки регулятора
и выбрать в качестве первого приближения настройки регулятора  исходя из физической реализации того или иного регулятора. Рассчитаем переходной процесс в результате которого полученное значение выхода регулятора
исходя из физической реализации того или иного регулятора. Рассчитаем переходной процесс в результате которого полученное значение выхода регулятора  и выхода ОР
и выхода ОР  . Затем проводится расчет численных значений частных производных выхода регулятора и объекта по оптимизируемым настройкам
. Затем проводится расчет численных значений частных производных выхода регулятора и объекта по оптимизируемым настройкам
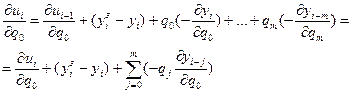
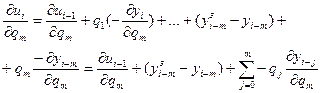


 (8)
(8)
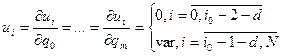

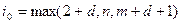
 на первой итерации приближения не может быть рассчитан по правилу (6), в качестве его начальных значений можно принять:
на первой итерации приближения не может быть рассчитан по правилу (6), в качестве его начальных значений можно принять:



