Использование оператора сдвига z для описания дискретных систем
Как известно из теории управления динамические звенья в аналоговой форме могут описываться с помощью дифференциальных уравнений и передаточных функций. По аналогии с этим, дискретные системы, описываемые конечно-разностными уравнениями с постоянными коэффициентами, могут быть описаны дискретными передаточными функциями, получаемыми с помощью оператора сдвига z.
Представление с помощью оператора сдвига z дает возможность компактного описания динамического звенья, а также проведение различных структурных преобразований для получения передаточной функции (описания) каких-либо соединений. Например, для получения передаточной функции замкнутой одноконтурной системы. Для объекта первого порядка с запаздыванием дискретная передаточная функция может быть получена:
Получение передаточной функции с использованием сдвига z для регуляторов аналогично. Для регулятора первого порядка примет вид:
Для объекта порядка n и регулятора порядка m дискретная передаточная функция примут вид:
Получим дискретную передаточную функцию для одноконтурной ЦСР при этом объект описывается конечно-разностным уравнением второго порядка без запаздывания, а регулятор реализует цифровой интегральный закон
В общем виде передаточную функцию любого соединения динамических звеньев можно представить в виде: Используя обратное z преобразование можно от дискретной передаточной функции соединения перейти к конечно-разностному уравнению этого соединения:
где
По передаточной функции замкнутой системы можно определить свойства этого соединения, такие как устойчивость, а также задавая начальные условия можно рассчитать переходной процесс замкнутой системы прямое и образование преобразование оператора z, как преобразование Лапласа используется для упрощения структурных преобразований системы.
|

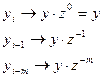
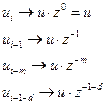


 - дискретная передаточная функция первого порядка с запаздыванием
- дискретная передаточная функция первого порядка с запаздыванием
 - дискретная передаточная функция регулятора первого порядка
- дискретная передаточная функция регулятора первого порядка

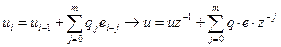





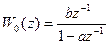








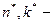 порядки знаменателя и числителя дискретной передаточной функции соединения
порядки знаменателя и числителя дискретной передаточной функции соединения коэффициенты дискретной передаточной функции соединения
коэффициенты дискретной передаточной функции соединения целое число тактов запаздывания соединения
целое число тактов запаздывания соединения


