Синтез комбинированных ЦСР
Синтез комбинированных систем должен обеспечить выполнение следующих требований: 1. поддержание регулируемой величины на заданном значении 2. обеспечение желаемых динамических свойств систем Данным требованиям удовлетворяет одноконтурная система регулирования с отрицательной обратной связью:
Однако, наличие возмущающего воздействия f, оказывающего влияние на выход объекта приводит к негативным последствиям:
Оба недостатка обусловлены самим принципом работы одноконтурной системы регулирования, который заключается в том, что регулируемое воздействие устраняющее влияние возмущения на выход объекта вырабатывается только тогда, когда возникает сигнал рассогласования. В этом случае улучшить качество переходного процесса объекта с возмущением можно путем использования следующих систем:
В этих системах реализуется принцип предварения, т.е. в момент возникновения возмущения оно измеряется, вырабатывается управляющее воздействие, которое на выходе объекта компенсирует влияние возмущения.
Используя дискретные передаточные функции элементов системы опишем ее работу следующей системой уравнений:
Используя подстановку преобразуем систему (1.1) к одному уравнению, связывающему выход системы у с ее входами
Анализ полученного выражения (1.3) в зависимости выхода системы у от ее входов (
2.1. раздельная оптимизация регулятора и компенсатора 2.2. одновременная оптимизация регулятора и компенсатора Рассмотрим данные подходы к расчету комбинированной системы подробнее. Принцип инвариантности заключается в таком расчете управляющей части комбинированной системы, при котором обеспечивается полная независимость выхода системы у от возмущающего воздействия f. Анализ выражения (1.3) показывает, что для выполнения данного условия при наличии возмущения отличного о нуля необходимо, чтобы нулю равнялась передаточная функция, стоящая перед ним:
Таким образом для выполнения принципа инвариантности необходимо, чтобы компенсатор возмущения рассчитывался по полученной зависимости (1.6), при этом к моменту его расчета передаточные функции по каналам возмущения и управления должны быть известны, например получены на этапе идентификации. Отсюда первым достоинством инвариантности комбинированной системы регулирования является полная независимость выхода у от возмущения
Исходя из выражения (1.7) комбинированная система регулирования может быть представлена следующей эквивалентной структурной схемой:
Из приведенной схемы следует, что вторым существенным достоинством инвариантности комбинированной ЦСР является то, что параметры (настройки) регулятора в этой системе могут определяться (рассчитываться) по каналу возмущения и компенсатора, т.е. как в одноконтурной системе, включающей регулятор и объект по каналу управления.
Недостатки синтеза инвариантной комбинированной системы 1. возможность компенсации только измеряемых возмущений 2. ограниченное число измеряемых компенсированных возмущений 3. невозможность физической реализации инвариантных компенсаторов в ряде случаев
Из полученного выражения следует, что инвариантный компенсатор может быть реализован, когда запаздывание по каналу управления не превышает запаздывание по каналу возмущения, в противном случае будет получено положительной запаздывание, что приводит к необходимости (как следует из конечно-разностного уравнения компенсатора) расчет текущего значения выхода инвариантного компенсатора на основе будущих значений его выхода, что физически реализовано быть не может. 4. порядок числителя передаточной функции компенсатора должен быть не больше порядка его знаменателя.
Второй подход (раздельная настройка регулятора и компенсатора комбинированной инвариантной системы регулирования) осуществляется следующим образом: 1. сначала в одноконтурной системе регулирования на основе канала управления осуществляется настройка регулятора (смотри алгоритм оптимизации одноконтурной системы) 2. настройка компенсатора осуществляется в комбинированной системе, включающей каналы управления и возмущения, регулятор с найденными оптимальными настройками и компенсатор с оптимизационными настройками. Анализ выражения (1.3) показывает, что при таком последовательном (раздельном) способе настройки обеспечить оптимальное регулирование для заданных структур регуляторов и компенсаторов невозможно, поскольку при настройке регулятора не учитывается влияние на его работу возмущающего воздействия. В этом случае при настройке компенсатора система уравнений, описывающая переходные процессы в комбинированной системе будут иметь вид:
Используя данную систему конечно-разностных уравнений можно провести оптимизацию компенсатора порядка
Для расчета переходного процесса по системам уравнений (1.8) и (1.9) необходимо задать следующие начальные условия:
dmin=min(du,df) i0=max(nmax,dmax+2,mmax+1+dmax) Одновременная организация регулятора и компенсатора в комбинированной системе В этом случае комбинированная ЦСР описывается системой конечно-разностных уравнений (1.8). Разница заключается в том, что искомыми настройками являются не только настройки компенсатора
Отсюда следует, что для нахождения численных значений частных производных критерия по настройкам регулятора и компенсатора, необходимо продифференцировать каждое из уравнений системы (1.8) по настройкам регулятора и компенсатора. Тогда система конечно-разностных уравнений будет выглядеть следующим образом:
Для расчета по приведенным конечно-разностным уравнениям, а также для расчета переходного процесса по системе уравнений (1.8), необходимо задать начальные условия, которые будут аналогичны для предыдущего алгоритма. Сама схема алгоритма одновременной оптимизации имеет такой же вид, как и алгоритм оптимизации в одноконтурных системах. Замечание: несмотря на то, что инвариантные комбинированные системы являются наилучшими, они не лишены своих недостатков, которые заключаются в невозможности их физической реализации в ряде случаев в частности:
Инвариантный компенсатор может быть реализован только в тех случаях, когда запаздывание по каналу возмущения больше, чем запаздывание по каналу управления. В противном случае
|




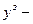 задание,
задание, 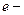 ошибка,
ошибка,  возмущение,
возмущение, 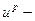 суммарное управляющее воздействие,
суммарное управляющее воздействие,  выход по каналу управления и возмущения,
выход по каналу управления и возмущения, 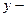 регулируемая величина,
регулируемая величина, 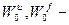 передаточная функция по каналу управления и возмущения,
передаточная функция по каналу управления и возмущения, 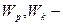 передаточная функция регулятора и компенсатора.
передаточная функция регулятора и компенсатора. (1.1)
(1.1)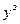 и
и 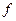 :
: (1.2)
(1.2)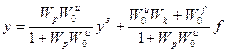 (1.3)
(1.3)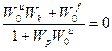 (1.4)
(1.4)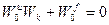 (1.5)
(1.5)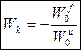 (1.6)- формула для расчета инвариантного компенсатора возмущения
(1.6)- формула для расчета инвариантного компенсатора возмущения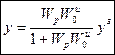 (1.7)
(1.7)
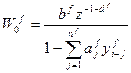
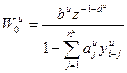
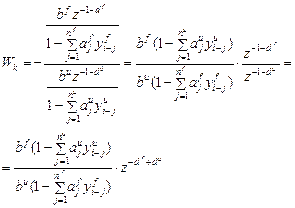
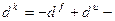 запаздывание инвариантного компенсатора
запаздывание инвариантного компенсатора (1.8)
(1.8)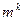 . При этом алгоритм оптимизации содержит те же самые этапы, что и алгоритм оптимизации в одноконтурной системе. Разница заключается только в системе конечно-разностных уравнений переходного процесса. При использовании для расчета частных производных критерии по настройкам компенсатора связанных рекуррентных зависимостей необходимо продифференцировать все уравнения системы (1.8) по всем настройкам компенсатора:
. При этом алгоритм оптимизации содержит те же самые этапы, что и алгоритм оптимизации в одноконтурной системе. Разница заключается только в системе конечно-разностных уравнений переходного процесса. При использовании для расчета частных производных критерии по настройкам компенсатора связанных рекуррентных зависимостей необходимо продифференцировать все уравнения системы (1.8) по всем настройкам компенсатора: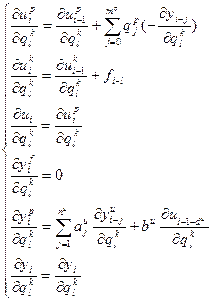
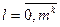

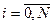
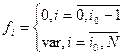
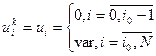

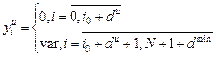
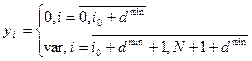
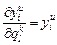

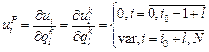
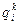 , но и настройки регулятора
, но и настройки регулятора 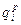 , поэтому оптимизация критерия ведется и по настройкам компенсатора и по настройкам регулятора, т.е.
, поэтому оптимизация критерия ведется и по настройкам компенсатора и по настройкам регулятора, т.е. 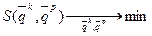 . Отсюда необходимым и достаточным условием существования минимума будет равенство нулю первых частных производных критерия по настройкам компенсатора и регулятора:
. Отсюда необходимым и достаточным условием существования минимума будет равенство нулю первых частных производных критерия по настройкам компенсатора и регулятора: 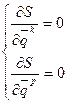 . Если в качестве критерия используется интегрально-квадратичная ошибка, то частные производные примут вид:
. Если в качестве критерия используется интегрально-квадратичная ошибка, то частные производные примут вид: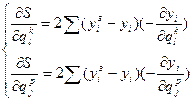
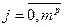
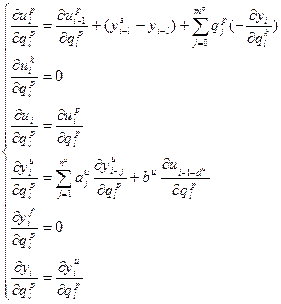
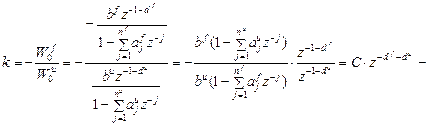 запаздывание инвариантного компенсатора
запаздывание инвариантного компенсатора
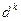 будет величиной, что физически не реализуемо (т.е. при положительном запаздывании компенсатора его текущее значение должно рассчитываться через будущее значение входа компенсатора, которое к настоящему моменту еще неизвестно).
будет величиной, что физически не реализуемо (т.е. при положительном запаздывании компенсатора его текущее значение должно рассчитываться через будущее значение входа компенсатора, которое к настоящему моменту еще неизвестно).


