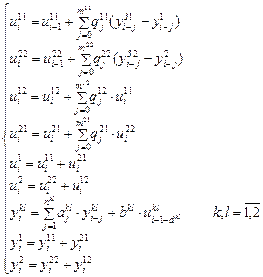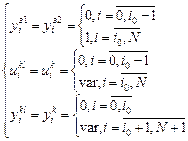Синтез системы связного регулирования
При сильных внутренних связях возможность получить высокое качество регулирования нужно искать не в корректировке настроек и структур регуляторов, а в развязывании внутренних связей по перекрестным каналам путем создания систем связного регулирования. При этом вводятся дополнительные внешние комплексные связи между регуляторами. Накладывать эти связи можно в различных местах: 1. между входом и выходом регуляторов или непосредственно между регулируемыми органами; 2. можно применять также смешанные связи. Теоретической основой для разработки рациональных схем связного регулирования является принцип автономности, предложенный современным ученым И.Н. Вознесенским: «Вводя внешние комплексные связи между регуляторами можно добиться расчленения сложной системы со многими взаимосвязанными параметрами на ряд простейших сепаратных систем, обладающих одним управляемым параметром каждая», т.е. другими словами, можно добиться того, чтобы каждая регулируемая величина системы
Это позволяет повысить скорость действия основных регуляторов, и, следовательно, улучшить качество регулирования. Недостатками автономных систем являются:
Исходя из вышесказанного, рассмотрим два основных подхода к расчету управляющей части при синтезе многосвязных систем регулирования:
Структурная схема двумерной системы связного регулирования имеет вид:
Первый и второй основные каналы: Первый и второй перекрестные каналы объекта: Примером функциональной схемы связного регулирования может являться система процесса ректификации:
Система уравнений, описывающая поведение системы связного регулирования с использованием дискретных передаточных функций имеет вид:
Получим уравнение взаимосвязи
Анализ выражения (3.5) показывает, что выход системы
В этом случае, при выполнении условия автономности, выход
Анализ выражения (3.7) показывает, что при выполнении принципа автономности, связанная двумерная система регулирования может быть представлена эквивалентной структурной схемой в виде совокупности двух одноконтурных систем.
В данном случае, несмотря на формальную схожесть принципа автономности для многосвязных и принципа инвариантности для комбинированных систем, между ними есть отличие. При выполнении принципа инвариантности в комбинированных системах в передаточную функцию объекта регулирования эквивалентной одноконтурной системы не входит передаточная функция по каналу возмущения, а только лишь передаточная функция по каналу управления; в связной системе при выполнении принципа автономности передаточную функцию объекта эквивалентной одноконтурной системы входит не только передаточная функция основного канала, но и передаточными функциями оставшихся трех каналов.
Покажем, что в автономной системе область устойчивого регулирования, а следовательно, и качество переходного процесса, увеличивается. Для этого рассмотрим случай, где Тогда выражение (3.7) примет вид:
Анализируя знаменатель полученного выражения (3.8) на основе критерия Найквиста, можно увидеть, что абсцисса критической точки смещается из -1 в -4/3. Таким образом, при выполнении принципа автономности произошло увеличение области устойчивого регулирования, что приводит к увеличению качества переходного процесса. Причем качество переходного процесса будет даже лучше, чем в одноконтурной системе, содержащей основной регулятор и один основной канал. При увеличении размерности системы в общем случае до
где
Правильность записи векторно-матричных уравнений и правильность структуры векторов и матриц проверяется на основе скалярной записи. Преимущества записи: 1. количество уравнений, входящих в нее, не зависит от размерности системы и остается постоянном, равным 4; 2. при увеличении размерности системы регулирования увеличивается размерность только векторов и матриц; 3. значительно упрощается выполнение преобразования.
Получим уравнение взаимосвязи вектора выходов и вектора заданий:
где
Получим условие автономности для векторно-матричной записи в общем виде, т.е для системы размерности
Условие автономности для векторно-матричной записи. Из подученного выражения следует, что для выполнения принципа автономности необходимо, чтобы матрица передаточных функций замкнутой системы была диагональной. Т.К. первая матрица Существует два подхода к расчету автономных систем компенсаторов из выше приведенного условия:
Решение данной системы уравнений с учетом приведенной скалярной записи вызывает трудности. Поэтому представим данную систему уравнений с использованием векторно-матричного описания:
Если матрица
Полученная зависимость (4.2) позволяет выполнить расчет дискретных передаточных функций компенсаторов из условия автономности.
Из выражения (4.3) следует:
Из выражения (4.4) следует, что диагональные элементы матричных компенсаторов в общем случае не равны единице, а являются некими дробно-рациональными выражениями, в отличии от первого подхода. Поэтому при расчете автономных компенсаторов по второму подходу по зависимости (4.4), их количество увеличится на r штук, в отличии от первого подхода. Структурная схема системы при втором подходе будет иметь вид (на примере двухмерной):
Основное отличие в том, что появляются компенсаторы по основным каналам
Поскольку матрица
Из (4.6) следует: r-мерная связная система при выполнении условия автономности может быть представлена эквивалентной структурной схемой в виде совокупности r одноконтурных систем:
В каждую из указанных одноконтурных систем входит соответствующий регулятор и эквивалентный объект с передаточной функцией При втором подходе передаточные функции эквивалентных объектов равны: Анализ выражений (4.2)-(4.7) позволяет указать достоинства и недостатки рассмотренных подходов. Достоинства первого подхода: 1. более простая структура компенсаторов перекрестных связей 2. наименьшее количество компенсаторов перекрестных связей Достоинства второго подхода: 1. возможность расчета таких компенсаторов перекрестных связей, которые обеспечивают требуемые динамические свойства эквивалентных объектов регулирования, т.е. при втором подходе мы самостоятельно залаем динамику эквивалентных объектов.
Автономные системы имеют ограничения на реализацию: 1. запаздывание автономных компенсаторов не должно быть положительным (по аналогии с инвариантным компенсатором в комбинированной системе) 2. матрица объекта должна быть невырожденной.
При одновременной оптимизации регуляторов и компенсаторов заданных структур в двумерной системе получим следующую систему уравнений:
Начальные условия:
Где i0=max(nkl,mkl,1+dkl) В этом случае частные производные критерия ищутся по настройкам всех регуляторов и всех компенсаторов.
|

 зависела только от одного входа системы
зависела только от одного входа системы  . В результате может быть достигнута полная компенсация влияния внутренних динамических связей между выходом. В этом случае изменении одного из управляющих параметров не вызовет изменения остальных, если другие источники возмущений стабилизированы. Достоинствами автономного регулирования являются:
. В результате может быть достигнута полная компенсация влияния внутренних динамических связей между выходом. В этом случае изменении одного из управляющих параметров не вызовет изменения остальных, если другие источники возмущений стабилизированы. Достоинствами автономного регулирования являются:

 задание по первому и второму выходу системы
задание по первому и второму выходу системы ошибка регулирования
ошибка регулирования выходы первого и второго основных регуляторов соответственно
выходы первого и второго основных регуляторов соответственно выходы первого и второго компенсаторов перекрестных связей
выходы первого и второго компенсаторов перекрестных связей суммарные управляющие воздействия (входы объекта)
суммарные управляющие воздействия (входы объекта) выходы по первому и второму основным каналам объекта соответственно
выходы по первому и второму основным каналам объекта соответственно основные регуляторы с передаточными функциями
основные регуляторы с передаточными функциями 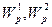 соответственно
соответственно компенсаторы перекрестных связей с передаточными функциями
компенсаторы перекрестных связей с передаточными функциями  соответственно
соответственно
 .
.
 (3.2)
(3.2)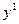 с входами
с входами  и
и  :
: (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5)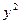 были равны нулю. Анализ этих слагаемых показывает, что дробно-рациональные выражения, стоящие в них, равны по модулю и отличны по знаку. В соответствии с принципом автономности, для того, чтобы второе и третье слагаемые были равны нулю, необходимо, чтобы равны были нулю числители:
были равны нулю. Анализ этих слагаемых показывает, что дробно-рациональные выражения, стоящие в них, равны по модулю и отличны по знаку. В соответствии с принципом автономности, для того, чтобы второе и третье слагаемые были равны нулю, необходимо, чтобы равны были нулю числители:
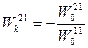 (3.6)- формула расчета автономного компенсатора перекрестной связи 21
(3.6)- формула расчета автономного компенсатора перекрестной связи 21 (3.7)
(3.7)


 (3.8)
(3.8) количества входов и выходов, можно использовать приведенное выше скалярное описании е для вывода формул расчета автономных компенсаторов и эквивалентных объектов не представляется возможным ввиду ее громоздкости (большое количество уравнений). В этом случае разрешить данную проблему позволяет использование векторно-матричного описания. Рассмотрим его вывод на примере двумерной системы:
количества входов и выходов, можно использовать приведенное выше скалярное описании е для вывода формул расчета автономных компенсаторов и эквивалентных объектов не представляется возможным ввиду ее громоздкости (большое количество уравнений). В этом случае разрешить данную проблему позволяет использование векторно-матричного описания. Рассмотрим его вывод на примере двумерной системы:
 вектор ошибки, равный
вектор ошибки, равный  ;
; вектор задания;
вектор задания; вектор измеряемых управляемых величин;
вектор измеряемых управляемых величин; вектор выходов регуляторов;
вектор выходов регуляторов; вектор управляющих воздействий;
вектор управляющих воздействий; диагональная матрица регуляторов;
диагональная матрица регуляторов; матрица компенсаторов;
матрица компенсаторов; матрица объектов.
матрица объектов.

 (3.9)
(3.9) матрица передаточных функций замкнутой системы;
матрица передаточных функций замкнутой системы; единичная матрица, соответствующей размерности.
единичная матрица, соответствующей размерности. , где
, где  . Представим выражение (3.9) в развернутом виде:
. Представим выражение (3.9) в развернутом виде:
 является диагональной, то должна быть диагональной матрица
является диагональной, то должна быть диагональной матрица  . Т.к. матрица регуляторов
. Т.к. матрица регуляторов 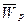 также диагональная, то в конечном виде условие автономности формируется, как диагональность произведения матриц
также диагональная, то в конечном виде условие автономности формируется, как диагональность произведения матриц  (4.0).
(4.0). на
на  , берутся не диагональные элементы результирующей матрицы и приравниваются к нулю. Таким образом приходим к системе линейных неоднородных уравнений относительно передаточных функций компенсаторов. Эта система имеет вид:
, берутся не диагональные элементы результирующей матрицы и приравниваются к нулю. Таким образом приходим к системе линейных неоднородных уравнений относительно передаточных функций компенсаторов. Эта система имеет вид:

 , (4.1) где
, (4.1) где  блочная матрица, элементами которой являются матрицы передаточных функций основных и перекрестных каналов объекта;
блочная матрица, элементами которой являются матрицы передаточных функций основных и перекрестных каналов объекта;  блочный вектор, элементами которого являются векторы передаточных функций компенсаторов;
блочный вектор, элементами которого являются векторы передаточных функций компенсаторов;  блочный вектор, элементами которого являются векторы передаточных функций перекрестных каналов объекта;
блочный вектор, элементами которого являются векторы передаточных функций перекрестных каналов объекта;  нулевой вектор.
нулевой вектор.


 матрица, полученная из матрицы объекта
матрица, полученная из матрицы объекта  не вырождена, то существует единственное решение уравнения (4.1):
не вырождена, то существует единственное решение уравнения (4.1): (4.2)
(4.2) (4.3), где
(4.3), где  диагональная матрица, задаваемая разработчиком.
диагональная матрица, задаваемая разработчиком. (4.4)
(4.4)
 и
и  . При выполнении условия автономности, когда произведение
. При выполнении условия автономности, когда произведение  является диагональной матрицей, получим и вектора задания:
является диагональной матрицей, получим и вектора задания: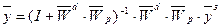 (4.5)
(4.5) диагональная:
диагональная: , то матрица замкнутой системы будет иметь вид:
, то матрица замкнутой системы будет иметь вид:  (4.6)
(4.6) . При первом подходе к расчету автономных компенсаторов передаточные функции эквивалентных объектов определяются из уравнения:
. При первом подходе к расчету автономных компенсаторов передаточные функции эквивалентных объектов определяются из уравнения:  (4.7)
(4.7) .
.