Определение независимых начальных условий.
Определение независимых начальных условий.
До коммутации в цепи был включён источник постоянного напряжения. На постоянном токе индуктивность обладает нулевым сопротивлением, а ёмкость – бесконечно большим. В эквивалентной схеме цепи для расчёта независимых начальных условий, изображённой на рис. 2, реактивные элементы показаны как короткое замыкание и обрыв.
Ток в цепи с индуктивностью определится выражением
Напряжение на ёмкости:
Согласно законам коммутации, ток в индуктивности и напряжение на ёмкости в момент коммутации не могут измениться скачком. Следовательно,
2. Операторная расчётная схема. При составлении операторной схемы замещения все элементы цепи замещаются их операторными эквивалентами. Так, индуктивность замещается операторным индуктивным сопротивлением pL, ёмкость – операторным ёмкостным сопротивлением 1/pС; активное сопротивление не изменяется. При этом ненулевые начальные условия учитываются в цепях с индуктивностью и с ёмкостью дополнительными источниками ЭДС. (рис 3).
Операторная схема замещения послекоммутационной цепи для рассматриваемого примера, построенная в соответствии с изложенным выше, приведена на рис. 4.
3. Уравнения цепи в операторной форме. Расчёт операторных изображений искомых функций.
Для расчёта операторной схемы замещения может быть применён любой известный метод: метод узловых потенциалов, метод наложения, метод контурных токов и т.д. Однако целесообразно использовать метод контурных токов, который при надлежащем выборе независимых контуров обеспечивает наиболее быстрое получение конечного результата. Выберем независимые контуры таким образом, чтобы общая ветвь содержала только сопротивление Уравнения, описывающие цепь на рис.4 по методу контурных токов, запишутся в виде
Решая полученную систему с помощью определителей, получим
Разделив числитель и знаменатель в двух последних выражениях на
Ёмкость на операторной схеме замещения цепи изображается операторным сопротивлением и источником ЭДС, учитывающим ненулевые начальные условия. Поэтому выражение для операторного напряжения на ёмкости запишется в виде
После подстановки получим
|


 А.
А. В.
В. А;
А; В.
В.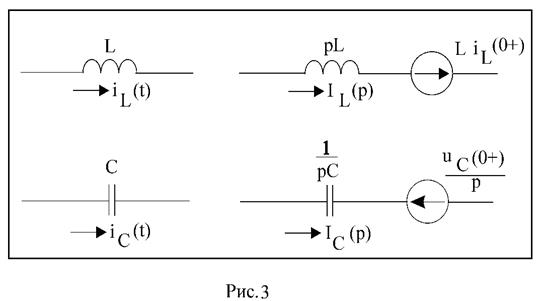

 . Тогда контурные токи
. Тогда контурные токи  и
и  будут равны изображениям токов в ёмкости и в индуктивности.
будут равны изображениям токов в ёмкости и в индуктивности. ;
;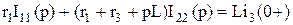 .
. ;
; .
. и подставив численные значения, получим
и подставив численные значения, получим ;
; .
. .
. .
.


