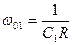Расчет передаточной функции первого звена фильтра.
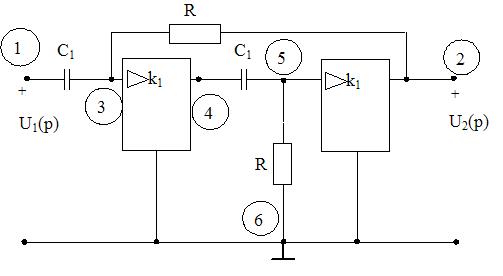
Принципиальная схема электрической цепи звена представлена на рис.2.1.
Рис.2.1
Представим схему замещения первого звена (рис. 2.2).
Рис.2.2 2.1.1.Узловые уравнения 1-го звена в общем виде.
Выберем узел №6 в качестве опорного узла. Тогда U6(p) = U0(p)=0. Для выходных узлов узловое уравнение не может быть составлено, так как при нулевых выходных сопротивлениях идеальных усилителей их выходные проводимости равны бесконечности. Поэтому для расчета передаточной функции достаточно записать уравнения для узлов (3) и (5):
Узел №3:
Узел №5:
Как было сказано выше, в электрических цепях, содержащих идеальные усилители, узловое уравнение для выходного узла не составляют. Вместо этого рекомендуется использовать уравнение связи. Для данного звена нужно составить два уравнения связи:
2.1.2.Расчёт коэффициентов левой части уравнений (2.2) и (2.3).
2.1.3. Расчёт правой части уравнений.
2.1.4.Уравнения (2.2) – (2.5) с учетом найденных коэффициентов.
2.1.5. Расчет передаточной функции первого звена.
Из уравнения (2.9) выразим
Выражения (2.8) и (2.10) подставим в (2.7) и выразим
Уравнение (2.11) подставим в (2.6) и выразим
В результате решения уравнений найдем передаточную функцию звена:
Преобразуем выражение для передаточной функции. С этой целью разделим числитель и знаменатель на коэффициент
Знаменатель передаточной функции звена содержит характеристический полином второго порядка, формально совпадающий с характеристическим полиномом резонансного колебательного контура.
где Аналогичные коэффициенты знаменателя передаточной функции звена называются добротностью и частотой полюса:
Численно они будут посчитаны ниже.
|



 (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5) ,
, 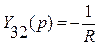 ,
,  ,
,  ,
,  ,
, ,
, 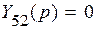 ,
, 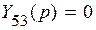 ,
,  ,
,  .
. ,
, 
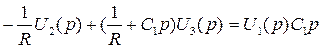 (2.6)
(2.6)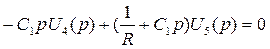 (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) :
: , (2.10)
, (2.10)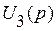 :
: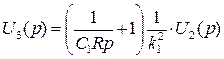 , (2.11)
, (2.11) через
через  :
: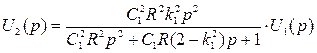 , (2.12)
, (2.12) , (2.13)
, (2.13) при операторе
при операторе 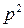 :
: , (2.14)
, (2.14)
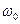 и
и  - резонансная частота и добротность контура соответственно.
- резонансная частота и добротность контура соответственно.
 ,
,