Передаточная функция и основные характеристики фильтров
Обычно фильтр анализируется как конечная линейная электронная схема с сосредоточенными параметрами. Если фильтр построен на активных элементах (операционные усилители), то, поскольку такая схема фильтра явно будет нелинейной, на первом этапе анализа она линеаризуется и далее рассматривается как линейная. Поведение такого фильтра (рис.1.5)
Рис.1.5
определяется передаточной функцией
где: p = jω ─ комплексная частотная переменная; ω ─ угловая частота, рад/с; a i, i = 0, …, n; b i, i = 0, …, m ─ вещественные коэффициенты. Подставив в формулу (1.1) значение комплексной частоты, получим комплексную передаточную функцию, которая определяет реакцию фильтра на синусоидальный сигнал. Модуль комплексной передаточной функции |H(jω)|=H(ω)─ амплитудно-частотная характеристика (АЧХ), а её аргумент arg (H(jω))= Числитель и знаменатель H(p) формулы (1.1) можно записать в виде произведения сомножителей первого порядка:
H(p) = где
График АЧХ передаточной функции изображают как в линейном, так и в логарифмическом масштабах. На оси ординат графика, построенного в линейном масштабе указывают модуль | H(j построенного в логарифмическом масштабе, принято откладывать значение 20lg | H(j Фазовый сдвиг Обе зависимости, построенные в широком диапазоне частот, определяют характер преобразования сигналов и тип фильтра: фильтр нижних частот (ФНЧ), фильтр верхних частот (ФВЧ), полосовой фильтр (ПФ), заграждающий фильтр (ЗФ) и другие типы фильтров с более сложным видом частотных характеристик. Для рассматриваемого в курсовой работе электрического фильтра передаточная функция имеет вид:
где
Расчет передаточных функций электрического фильтра и составляющих его звеньев производится, как было отмечено выше, путем формирования и решения узловых уравнений в операторной форме. Формирование уравнений электрической цепи с идеальными усилителями [2] имеет следующие особенности: - при формировании уравнения для входного узла влияние усилителя не учитывается, так как ток во входной ветви идеального усилителя равен нулю; - для выходного узла узловое уравнение не может быть составлено, так как при нулевом выходном сопротивлении идеального усилителя его выходная проводимость равна бесконечности; - систему узловых уравнений необходимо дополнить уравнением связи входного и выходного напряжений усилителя в результате получим систему, в которой число уравнений равно числу неизвестных. Напряжение на входе и выходе усилителя с конечным коэффициентом усиления связаны уравнением:
где
Если коэффициент усиления задан равным бесконечности, то при конечной величине напряжения
При анализе цепей с дифференциальным операционным усилителем с бесконечным коэффициентом усиления система узловых уравнений должна быть дополнена уравнением:
Составим узловые уравнения для электрической цепи, приведённой на рис. 1.5. и являющейся типовой схемой одного из звеньев каскадной реализации активного фильтра Для расчета передаточной функции достаточно записать уравнения для узлов (3) и (4):
Узловое уравнение для выходного узла не составляют. Вместо этого рекомендуется использовать уравнение:
С учётом найденных коэффициентов, уравнения примут вид:
В результате решения уравнений найдем передаточную функцию звена:
Преобразуем выражение для передаточной функции. С этой целью разделим числитель и знаменатель на коэффициент
Знаменатель передаточной функции звена содержит характеристический полином второго порядка, формально совпадающий с характеристическим полиномом резонансного колебательного контура.
где Аналогичные коэффициенты знаменателя передаточной функции звена называются добротностью и частотой полюса:
Подставив в выражение для H(p) значение комплексной частоты
После чего определяют выражения и строят графики частотных характеристик модуля (АЧХ) и аргумента (ФЧХ) передаточной функции (смотри приложение).
Приложение. СХЕМА АКТИВНОГО RC – ФИЛЬТРА.
Схема фильтра представлена на рис.1.1.
Рис.1.1
Номиналы элементов: R = 100 кОм C1 = 1,8 нФ С2= 1,2 нФ k1 = 1,2 k2=1,4
|


 , равной отношению операторного изображения выходной величины U2(p) к операторному изображению входной величины U1(p) то есть определяется отношением двух полиномов от комплексной переменной «р» [1]:
, равной отношению операторного изображения выходной величины U2(p) к операторному изображению входной величины U1(p) то есть определяется отношением двух полиномов от комплексной переменной «р» [1]: H(p) =
H(p) = 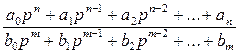 (1.1)
(1.1) (ω) ─ фазочастотная характеристика (ФЧХ). Расчет выражений для АЧХ (модуля передаточной функции) и ФЧХ (аргумента передаточной функции) производится в обычном порядке, как расчет модуля и аргумента комплексного числа.
(ω) ─ фазочастотная характеристика (ФЧХ). Расчет выражений для АЧХ (модуля передаточной функции) и ФЧХ (аргумента передаточной функции) производится в обычном порядке, как расчет модуля и аргумента комплексного числа. ,
,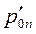 - корни полинома числителя (их принято называть нулями передаточной функции);
- корни полинома числителя (их принято называть нулями передаточной функции); - корни полинома знаменателя (их принято называть полюсами передаточной функции).
- корни полинома знаменателя (их принято называть полюсами передаточной функции). |. На оси ординат графика АЧХ,
|. На оси ординат графика АЧХ, ,
, -передаточная функция по напряжению первого звена фильтра;
-передаточная функция по напряжению первого звена фильтра; -передаточная функция по напряжению второго звена фильтра.
-передаточная функция по напряжению второго звена фильтра. ,
, -операторное напряжение на входе;
-операторное напряжение на входе; -операторное напряжение на выходе;
-операторное напряжение на выходе; -коэффициент усиления.
-коэффициент усиления.
 , где
, где


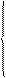

 .
.
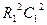 при операторе
при операторе  :
:
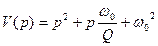 ,
, и
и  - резонансная частота и добротность контура соответственно.
- резонансная частота и добротность контура соответственно.


 , получим комплексную передаточную функцию:
, получим комплексную передаточную функцию:




