Вычисление определителя привидением к треугольному виду
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется. Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на
В полученной матрице нужно сделать равными нулю элементы Осталось сделать равным нулю элемент 2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:
|

 приводя его к треугольному виду.
приводя его к треугольному виду. первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4): , т.е. умножить на (-2):
, т.е. умножить на (-2): и
и 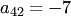 второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента
второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента  и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно: . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
. К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):


