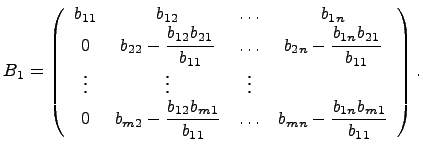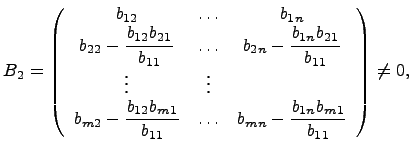а) Так как  , то в матрице A существует элемент
, то в матрице A существует элемент  . Если
. Если  , то переходим к пункту «б». Если
, то переходим к пункту «б». Если  , то, поменяв в матрице A местами
, то, поменяв в матрице A местами  -ю и
-ю и  -ю строки, а затем, в полученной матрице поменяв местами
-ю строки, а затем, в полученной матрице поменяв местами  -й и
-й и  -й столбцы, получим матрицу
-й столбцы, получим матрицу  , в которой элемент в позиции (1, 1) -
, в которой элемент в позиции (1, 1) -  .
.
б) Элемент  назовём ведущим элементом первого шага. С его помощью аннулируем все расположенные под ним элементы 1-го столбца. Для этого из каждой строки, начиная со второй, вычтем первую строку, умноженную на
назовём ведущим элементом первого шага. С его помощью аннулируем все расположенные под ним элементы 1-го столбца. Для этого из каждой строки, начиная со второй, вычтем первую строку, умноженную на  ,
,  , …,
, …,  соответственно.
соответственно.
После выполнения первого шага матрица переходит в матрицу
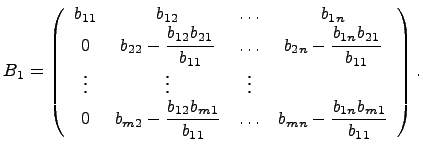
Если при этом все строки, начиная со второй, стали нулевыми, то весь процесс завершается, так как матрица уже приведена к верхней трапециевидной форме. Если же в этих строках есть хотя бы один, отличный от нуля элемент, т.е. если матрица
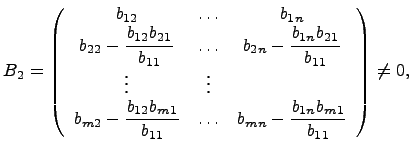
то переходим ко второму шагу.

 , то в матрице A существует элемент
, то в матрице A существует элемент  . Если
. Если  , то переходим к пункту «б». Если
, то переходим к пункту «б». Если  , то, поменяв в матрице A местами
, то, поменяв в матрице A местами  -ю и
-ю и  -ю строки, а затем, в полученной матрице поменяв местами
-ю строки, а затем, в полученной матрице поменяв местами  -й столбцы, получим матрицу
-й столбцы, получим матрицу  , в которой элемент в позиции (1, 1) -
, в которой элемент в позиции (1, 1) -  .
. назовём ведущим элементом первого шага. С его помощью аннулируем все расположенные под ним элементы 1-го столбца. Для этого из каждой строки, начиная со второй, вычтем первую строку, умноженную на
назовём ведущим элементом первого шага. С его помощью аннулируем все расположенные под ним элементы 1-го столбца. Для этого из каждой строки, начиная со второй, вычтем первую строку, умноженную на  ,
,  , …,
, …,  соответственно.
соответственно.