Предположим, что это не верно тогда

получена бесконечная ограниченная последовательность x_n,из нее можно выбрать сходящуюся подпоследовательность 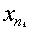, пусть ее предел равен x₀. Так как круг Е замкнут, то x₀ пренадлежит Е. Тогда так как f(x) непрерывна получено противоречие, следовательно неверно, предположение о неограничености f(x). Лемма №6. Действительная функция комплексного переменного f(x) непрерывная взамкнутом круге Е достигает своего минимума имаксимума. Доказательство. Докажем это утверждение для максимума.Так как f(x) непрерывна в Е, то она ограничена и следовательносуществует M = sup{ f(x)}. Рассмотрим функцию .Если f(x) не достигает своего максимума, то M> f(x) следовательно M-f(x)>0, следовательно g(x) непрерывна в Е. Полученое противоречит тому, что M = sup{ f(x)}. Следовательнофункция достигает свего максимума. Аналогично доказывается достижение минимума. Доказательство основной теоремы. Пусть дан многочлен f(x), очевидно что если a_n-свободный член, тоf(0)= a_n. Теперь применим лемму№3: возьмем М=|f(0)| =|a_n|тогда существует такое N, что при |x|>N |f(x)|>M. Теперь возьмем круг Еограниченный окружностью с центром в нуле и радиусом N, включая границы круга.Так как (по лемме №1) многочлен f(x)-непрерывен, то и |f(x)|-непрерывен внутризамкнутого круга Е, следовательно(по лемме №6), существует такая точка x₀, что для всех x из E выполняется неравенство |f(x)|>=|f(x₀)|. x₀ является точкой минимума для |f(x)| внутри E. Т.к для любого x:|x|>N|f(x)|>M>|f(0)|>|f(x₀)| точка x₀ является точкойминимуа |f(x)| на всей комплексной плоскости.|f(x₀)|=0 т.к по лемме Даламбера если |f(x₀)|¹0 то x₀ не точка минимума для |f(x)|Þ x₀-корень многочленаf(x).Теорема доказана.