Доказательство.
Докажем единственность. Предположим, что
Пусть
Получаем, что 2. Алгебраическая запись комплексного числа. Операции над комплексными числами, их св-ва? Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1.Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Два комплексных числа a+ bi и a – bi называются сопряжёнными комплексными числами. Основные договорённости: 1. Действительное число а может быть также записано в форме комплексного числа: a+ 0 i или a – 0 i. Например, записи 5 + 0 i и 5 – 0 i означают одно и то же число 5.
2. Комплексное число 0 + bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0 + bi.
3. Два комплексных числа a+ bi и c+ di считаются равными, если a= c и b= d. В противном случае комплексные числа не равны.
Сложение. Суммой комплексных чисел a+ bi и c+ di называется комплексное число (a+ c) + (b+ d) i. Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты. Это определение соответствует правилам действий с обычными многочленами.
Вычитание. Разностью двух комплексных чисел a+ bi (уменьшаемое) и c+ di (вычитаемое) называется комплексное число (a – c) + (b – d) i. Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a+ bi и c+ di называется комплексное число: (ac – bd) + (ad + bc) i. Это определение вытекает из двух требований:
1) числа a+ bi и c+ di должны перемножаться, как алгебраические двучлены, 2) число i обладает основным свойством: i 2 = – 1.
П р и м е р. (a+ bi)(a – bi) = a 2 + b 2. Следовательно, произведение двух сопряжённых комплексных чисел равно действительному положительному числу. Деление. Разделить комплексное число a+ bi (делимое) на другое c+ di (делитель) - значит найти третье число e+ f i (чатное), которое будучи умноженным на делитель c+ di, даёт в результате делимое a+ bi. Если делитель не равен нулю, деление всегда возможно. П р и м е р. Найти (8 + i): (2 – 3 i). Р е ш е н и е. Перепишем это отношение в виде дроби: Умножив её числитель и знаменатель на 2 + 3 i и выполнив все преобразования, получим:
3. Сопряжения и его свойства? Представление комплексного числа в виде
Число
Если Число
|

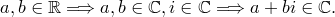
 — произвольный элемент
— произвольный элемент  . По аксиоме 4,
. По аксиоме 4, 


 . Пусть
. Пусть  не имеет вещественных корней и имеет отрицательный дискриминант.
не имеет вещественных корней и имеет отрицательный дискриминант.
 . Тогда
. Тогда
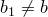 . Тогда
. Тогда
 . Это невозможно, значит,
. Это невозможно, значит,  . Тогда
. Тогда  .
.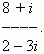

 называется каноническим представлением комплексного числа. Число
называется каноническим представлением комплексного числа. Число  называется вещественной частью числа
называется вещественной частью числа 

 называется мнимой частью числа
называется мнимой частью числа 
 , то число
, то число  , то
, то 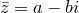 называется сопряженным с
называется сопряженным с 


