Определение поляРассмотрим систему
a2x + b2y + c2z = 0, a3x + b3y + c3z = 0.
Эта система называется однородной. Однородная система всегда имеет решение: x = y = z = 0 (тривиальное решение). C другой стороны, если определитель системы ∆ ≠ 0, то система имеет единственное решение. Следовательно, при ∆ ≠ 0 тривиальное решение является единственным. Если ∆ = 0, то система либо не имеет решений, либо имеет бесконечное множество решений. Но однородная система не может не иметь решений (x = y = z = 0 – решение), следовательно, при ∆ = 0 однородная система имеет бесконечное множество решений. П р и м е р. 2x + 3y – 5z = 0, ∆ = 0. x + 3y – 2z = 0,
- 3y – z = 0. действительное число.
Определение поля Определение. Полем называется непустое множество, для элементов которого определено два действия, называемых сложением и умножением, которые удовлетворяют следующим аксиомам: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Пример. Поля:
|
a1x + b1y + c1z = 0,
3x + 6y – 7z = 0.
x + 3y - 2z = 0, y = - z/3, x = -3y + 2z = 3z. Ответ: x = 3z, y = -z/3, z = z, где z –любое
(коммутативность сложения);
(ассоциативность сложения);
(существование нуля);
(существование противоположного элемента);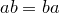
(коммутативность умножения);
(ассоциативность умножения);
(существование единицы);
(существование обратного элемента);
(дистрибутивность);
(в поле должно существовать хотя бы два элемента).
– поле вещественных чисел, 
– поле рациональных чисел,
