Рациональные корни многочлена с целыми коэффициентами. Пример. Основная теорема алгебры.
Рациональные корни многочленов с целыми коэффициентами Прежде, чем дать общую формулировку теоремы о рациональных корнях многочленов с целыми коэффициентами, решим следующую задачу. Задача. Найти все корни уравнения
являющиеся рациональными числами. Решение. Предположим, что рассматриваемое уравнение имеет корень, являющийся рациональным числом. Тогда, поскольку каждое рациональное число можно представить в виде несократимой дроби
где
Умножая это равенство на
Теперь преобразуем равенство (1):
Отсюда вытекает, что число Теперь преобразуем равенство (1) по-другому:
Значит, число Далее, рассматривая все возможные комбинации чисел
может принимать только следующие значения:
Таким образом, если у исходного уравнения и есть рациональный корень, то искать его нужно среди полученных шести чисел. Других рациональных корней у исходного уравнения быть не может. Подставляя поочередно каждое из этих чисел в исходное уравнение, получаем, что корнем уравнения является лишь число Оставляя читателю проверку того, что другие числа корнями исходного уравнения не являются, покажем, что число
Ответ. Число Замечание. Для того, чтобы найти все остальные корни исходного уравнения, нужно, воспользовавшись теоремой Безу, разделить многочлен
на двучлен
В результате деления получится квадратный трехчлен
после чего остается лишь решить квадратное уравнение:
Теорема. Если рациональное число (несократимая дробь)
где
все коэффициенты
которого являются целыми числами, то числитель дроби Коэффициент Основная теорема алгебры. Всякий многочлен с любыми комплексными коэффициентами, степень которого неменьше единицы имеет хотя бы один корень, в общем случае комплексный.
|

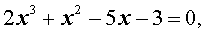
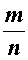 ,
,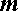 – число целое, а
– число целое, а 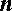 – число натуральное, то выполняется равенство:
– число натуральное, то выполняется равенство:
 , получаем равенство:
, получаем равенство: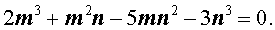
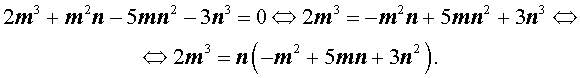
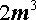 нацело делится на число
нацело делится на число 
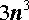 нацело делится на число
нацело делится на число 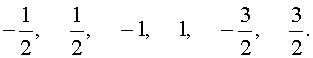
 .
.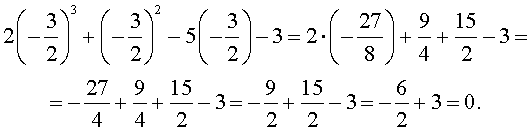
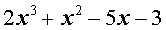

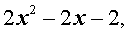

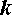 -ой степени
-ой степени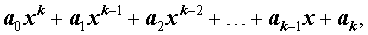
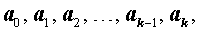
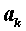 , а знаменатель дроби
, а знаменатель дроби 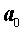 .
.


