Умножение матриц, свойства. Пример.
Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя. Пример. Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата
Элемент ci,j матрицы – ответа принадлежащий i -ой строке и j -му столбцу, вычисляется как произведение i-ой строки первого сомножителя An,m на j -ый столбец второго сомножителя Bm,k. Так, например, при вычислении элемента умножается первая строка на третий столбец, а при вычислении элемента умножается третья строка на первый столбец. Можно перемножать только те строки и столбцы, у которых одинаковое число элементов (смотри условие возможности умножения матриц). В результате получается число, равное сумме произведений соответствующих элементов (первый элемент строки на первый элемент столбца плюс второй элемент строки на второй элемент столбца и т. д. и, наконец, плюс произведение последних элементов). Рассмотрим умножение матриц на примере:
где
Пример. Отметим основные свойства операции произведения матриц.
1) В общем случае 2) 3) 4) При умножении любой квадратной матрицы на единичную первоначальная матрица не меняется 11. Транспонирование матриц, свойства. Обратная матрица и её свойства.
|
. Если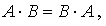 
то матрицы А и В называются перестановочными по отношению друг к другу.
