Доказательство. Поделим с остатком многочлен P(x) на многочлен x − a:
Поделим с остатком многочлен P (x) на многочлен x − a: P (x) = (x − a) Q (x) + R (x). Так как deg R (x) < deg(x − a) = 1, то R (x) — многочлен степени не выше 0. Подставляя x = a, поскольку (a − a) Q (a) = 0, имеем P (a) = R (a). Схема Горнера - один из простейших способов деления многочлена
Начнем заполнять пустые ячейки во второй строке. В первую пустую ячейку запишем 5, просто перенеся ее из соответствующей ячейки первой строки:
Следующую ячейку заполним по такому принципу:
Аналогично заполним и четвертую:
Для пятой ячейки получим
И, наконец, для последней, шестой ячейки, имеем
Задача решена, осталось только записать ответ:
Как видите, числа, расположенные во второй строке (между первым и последним), есть коэффициенты многочлена, полученного после деления
Полученный результат говорит также и о том, что 1 является корнем многочлена Приведем еще один пример. Разделим многочлен
Если наша цель - найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, - до тех пор, пока мы не исчерпаем все корни. Например, отыщем все корни многочлена
Итак, в остаче имеем 0, т.е. единица действительно является корнем данного мнгогочлена. Попробуем проверить единицу еще несколько раз. Новую таблицу для этого создавать не будем, а продолжим использование предыдущей:
Вновь в остаче ноль. Продолжим таблицу до тех пор, пока не исчерпаем все возможные значения корней:
Итог: Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целых корней метод довольно-таки неплох.
|

 на бином x-a. Конечно, делением применение схемы Горнера не исчерпывается, но для начала рассмотрим именно это. Применение алгоритма поясним на примерах. Разделим
на бином x-a. Конечно, делением применение схемы Горнера не исчерпывается, но для начала рассмотрим именно это. Применение алгоритма поясним на примерах. Разделим  на
на  . Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена
. Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 



 :
:
 :
:
 :
:

 . Следовательно, если в нашем случае остача равна нулю, то многочлены делятся нацело.
. Следовательно, если в нашем случае остача равна нулю, то многочлены делятся нацело.
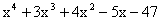 на
на  . Сразу оговорим, что выражение
. Сразу оговорим, что выражение  . В схеме Горнера будет учавствовать именно -3.
. В схеме Горнера будет учавствовать именно -3.
 . Целые корни нужно искать среди делителей свободного члена, т.е. среди делителей 8. Т.е., целыми корнями могут быть числа -8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:
. Целые корни нужно искать среди делителей свободного члена, т.е. среди делителей 8. Т.е., целыми корнями могут быть числа -8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:


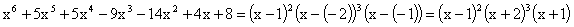 .
.


