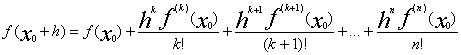Доказательство основной теоремы.
Лемма №1. Надо доказать, что

|
f(x0+x)-f(x0) |<
e. Докажем Лемму №1 сначала для многочлена без свободного члена и при x
0=0Если A=max(|a
0 |,|a
1|,.,|a
n-1|) и
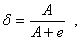
(1)то
|f(x)|=|a0xn+.+an-1x| 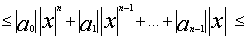
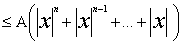
,
т.к |
x |<
б,и из (1)
б<1, тот.к. a
0=0 то f(0)=0

Что и требовалось доказать.Теперь докажем непрерывность любого многочлена.f(x
0+x)=a
0(x
0+x)
n+.+a
n pаскрывая все скобки по формуле бинома и собирая вместе члены содинаковыми степенями
x получим
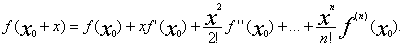
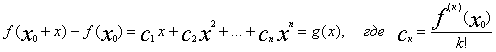
Многочлен g(x)-это многочлен от x при x
0 =0 и а
0=0
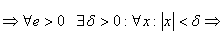 |f(x0+x)-f(x)|=|g(x)|<e
|f(x0+x)-f(x)|=|g(x)|<e Лемма доказана.
Лемма №2 Если дан многочлен
n -ой степени,
n>0, f(x)=a0xn+a1xn-1+.+an с произвольными комплексными коэффициентами и если
k - любоеположительное действительное число, то для достаточно больших по модулюзначений
x верно неравенство:
|a0xn|>k|a1xn-1+a2xn-2+..+an| (2) Доказательсво. Пусть А=max(

), тогда
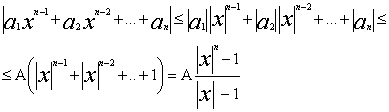
пологая |
x| >1, получим

откуда

следовательно неравенство (2) будет выполняться если |x|>1 и
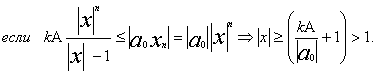
Лемма №2 доказана.
Лемма №3.

Доказательство.
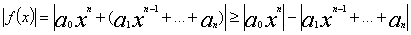
(3)применим лемму 2: при k=2 существует такое N
1, что при |x|> N
1 |a0xn|>2|a1xn-1+a2xn-2+..+an| откуда
|a1xn-1+a2xn-2+..+an|<|a0xn|/2 тогда из (3)

при |x|>N=max(N
1,N
2) |f(x)|>M что и тебовалось доказать.
Лемма №3(Лемма Даламбера). Если при
x=x0 многочлен
f(x) степени
n,

не обращаеться в нуль, то существует такое приращение h, в общем случаекомплексное, что
|f(x0+h)|<|f(x)| Доказательство.
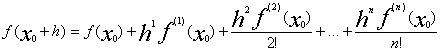
По условию f(x
0) не равно нулю, случайно может быть так, что x
0 является корнем f’(x),..,f
(k-1) (x). Пусть k-я производная будетпервой, не имеющей x
0 своим корнем. Такое k существует т.к.f
(n)(x
0)=n!a
0Таким образом
Т.к f(x
0) не равно нулю то поделим обе части уравнения на f(x
0)и обозначим
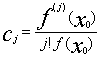
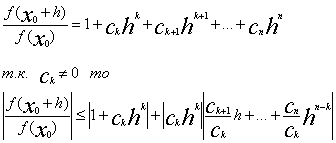
Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и егоаргумент.По лемме№1:

С другой стороны при
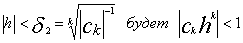
(4)Пусть |h|<min(
б1,
б2), тогда

Теперь выберем аргумент h так, чтобы c
kh
k былодействительным отрицательным числом.
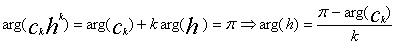
При таком выборе c
kh
k=-| c
kh
k| следовательно учитывая (4) получим

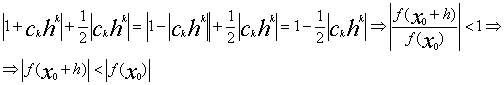
Что доказывает лемму Даламбера.
Лемма №5. Если действительная функция комплексного переменного
f(x) непрерывна взамкнутом круге Е, то она ограничена. Доказательство.
 | f(x0+x)-f(x0) |< e. Докажем Лемму №1 сначала для многочлена без свободного члена и при x0=0Если A=max(|a0 |,|a1|,.,|a n-1|) и
| f(x0+x)-f(x0) |< e. Докажем Лемму №1 сначала для многочлена без свободного члена и при x0=0Если A=max(|a0 |,|a1|,.,|a n-1|) и 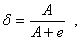 (1)то |f(x)|=|a0xn+.+an-1x|
(1)то |f(x)|=|a0xn+.+an-1x| 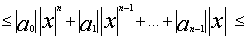
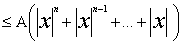 ,
,  Что и требовалось доказать.Теперь докажем непрерывность любого многочлена.f(x0+x)=a0(x0+x)n+.+an pаскрывая все скобки по формуле бинома и собирая вместе члены содинаковыми степенями x получим
Что и требовалось доказать.Теперь докажем непрерывность любого многочлена.f(x0+x)=a0(x0+x)n+.+an pаскрывая все скобки по формуле бинома и собирая вместе члены содинаковыми степенями x получим 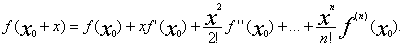
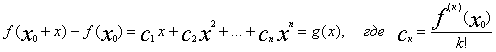 Многочлен g(x)-это многочлен от x при x0 =0 и а0=0
Многочлен g(x)-это многочлен от x при x0 =0 и а0=0 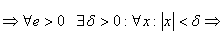 |f(x0+x)-f(x)|=|g(x)|<e Лемма доказана. Лемма №2 Если дан многочлен n -ой степени, n>0, f(x)=a0xn+a1xn-1+.+an с произвольными комплексными коэффициентами и если k - любоеположительное действительное число, то для достаточно больших по модулюзначений x верно неравенство: |a0xn|>k|a1xn-1+a2xn-2+..+an| (2) Доказательсво. Пусть А=max(
|f(x0+x)-f(x)|=|g(x)|<e Лемма доказана. Лемма №2 Если дан многочлен n -ой степени, n>0, f(x)=a0xn+a1xn-1+.+an с произвольными комплексными коэффициентами и если k - любоеположительное действительное число, то для достаточно больших по модулюзначений x верно неравенство: |a0xn|>k|a1xn-1+a2xn-2+..+an| (2) Доказательсво. Пусть А=max(  ), тогда
), тогда 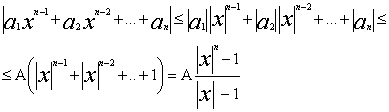 пологая | x| >1, получим
пологая | x| >1, получим  откуда
откуда  следовательно неравенство (2) будет выполняться если |x|>1 и
следовательно неравенство (2) будет выполняться если |x|>1 и 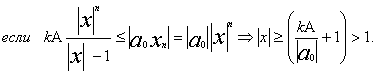 Лемма №2 доказана. Лемма №3.
Лемма №2 доказана. Лемма №3.  Доказательство.
Доказательство. 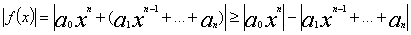 (3)применим лемму 2: при k=2 существует такое N1, что при |x|> N1 |a0xn|>2|a1xn-1+a2xn-2+..+an| откуда |a1xn-1+a2xn-2+..+an|<|a0xn|/2 тогда из (3)
(3)применим лемму 2: при k=2 существует такое N1, что при |x|> N1 |a0xn|>2|a1xn-1+a2xn-2+..+an| откуда |a1xn-1+a2xn-2+..+an|<|a0xn|/2 тогда из (3)  при |x|>N=max(N1,N2) |f(x)|>M что и тебовалось доказать. Лемма №3(Лемма Даламбера). Если при x=x0 многочлен f(x) степени n,
при |x|>N=max(N1,N2) |f(x)|>M что и тебовалось доказать. Лемма №3(Лемма Даламбера). Если при x=x0 многочлен f(x) степени n,  не обращаеться в нуль, то существует такое приращение h, в общем случаекомплексное, что |f(x0+h)|<|f(x)| Доказательство.
не обращаеться в нуль, то существует такое приращение h, в общем случаекомплексное, что |f(x0+h)|<|f(x)| Доказательство. 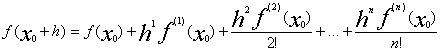 По условию f(x0) не равно нулю, случайно может быть так, что x0 является корнем f’(x),..,f(k-1) (x). Пусть k-я производная будетпервой, не имеющей x0 своим корнем. Такое k существует т.к.f(n)(x0)=n!a0Таким образом
По условию f(x0) не равно нулю, случайно может быть так, что x0 является корнем f’(x),..,f(k-1) (x). Пусть k-я производная будетпервой, не имеющей x0 своим корнем. Такое k существует т.к.f(n)(x0)=n!a0Таким образом 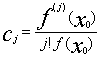
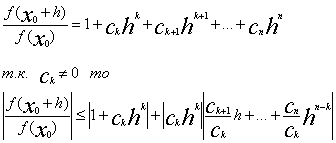 Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и егоаргумент.По лемме№1:
Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и егоаргумент.По лемме№1:  С другой стороны при
С другой стороны при 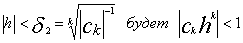 (4)Пусть |h|<min(б1, б2), тогда
(4)Пусть |h|<min(б1, б2), тогда  Теперь выберем аргумент h так, чтобы ckhk былодействительным отрицательным числом.
Теперь выберем аргумент h так, чтобы ckhk былодействительным отрицательным числом. 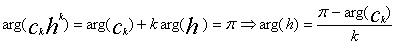 При таком выборе ckhk=-| ckhk| следовательно учитывая (4) получим
При таком выборе ckhk=-| ckhk| следовательно учитывая (4) получим 
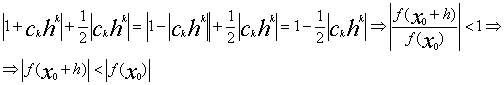 Что доказывает лемму Даламбера. Лемма №5. Если действительная функция комплексного переменного f(x) непрерывна взамкнутом круге Е, то она ограничена. Доказательство.
Что доказывает лемму Даламбера. Лемма №5. Если действительная функция комплексного переменного f(x) непрерывна взамкнутом круге Е, то она ограничена. Доказательство.