Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ;
Из определения следуют следующие формулы:
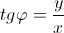
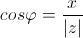
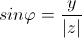
Для числа z = 0 аргумент не определен.
Главным значением аргумента называется такое значение φ, что 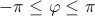 . Обозначается: arg(z).
. Обозначается: arg(z).
Свойства аргумента:
| 1.
| 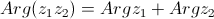
| - аргумент от произведения двух комплексных чисел равен сумме аргументов этих чисел
|
| 2.
| 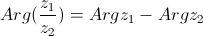
| - аргумент частного двух комплексных чисел равен разности аргументов этих чисел
|
| 3.
| 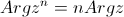
|
|
| 4.
| 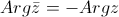
| - аргумент от сопряженного к комлексного числа равен отрицательному значению аргумента от этого числа.
|
Модулем комплексного числа z = x + iy называется вещественное число |z| равное:
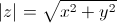
Для любых комплексных числе z, z1, z2 имеют место следубщие свойства модуля:
| 1.
| 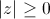 , причем |z| = 0 тогда и только тогда, когда z = 0 , причем |z| = 0 тогда и только тогда, когда z = 0
|
| 2.
| 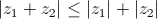 - неравенство треугольника для комплексных чисел - неравенство треугольника для комплексных чисел
|
| 3.
| 
|
| 4.
| 
|
| 5.
| для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости
|
ригонометрическая форма записи комплексного числа:
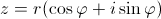
Показательная форма записи комплексного числа:
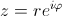
где r - модуль, а φ; - аргумент комплексного числа.
Для тригонометрической формы записи верны следующие свойства:
Для показательной формы записи справедливы следующие свойства:
Формула Муавра:
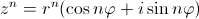
5. Извлечение корня n-степени из комплексного числа?
Корнем n -й степени из комплексного числа называется такое комплексное число, n -я степень которого равна подкоренному числу.
Таким образом, равенство:
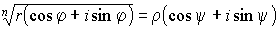
равносильно равенству
r n (cos n y + i sin n y) = r (cos j + i sin j)
Но у равных комплексных чисел модули должны быть равны, и аргументы могут отличаться лишь кратным 2p, т.е.
r n = r, n y = j + 2 k p,
откуда
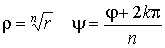
где  есть арифметическое значение корня и k - любое целое число. Таким образом мы получаем:
есть арифметическое значение корня и k - любое целое число. Таким образом мы получаем:

| (16)
|
т.е. для извлечения корня из комплексного числа надо извлечь корень из его модуля, а аргумент разделить на показатель корня.
В формуле (16) число k может принимать всевозможные целые значения; однако можно показать, что различных значений корня будет только n, и они будут соответствовать значениям:
| k = 0, 1, 2,..., (n -1)
| (17)
|
Чтобы доказать это, заметим, что правые части в формуле (16) будут различными при двух различных значениях k = k 1 и k = k 2 тогда, когда аргументы  и
и  отличаются не кратным 2p, и будут одинаковыми, если указанные аргументы отличаются кратным 2p.
отличаются не кратным 2p, и будут одинаковыми, если указанные аргументы отличаются кратным 2p.
Но разность (k 1 - k 2) двух чисел из ряда (17) по абсолютному значению меньше n, а потому разность
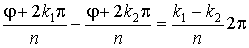
не может быть кратна 2p, т.е. n значениям k из ряда (17) соответствуют n различных значений корня.
Пусть теперь k 2 - целое число (положительное или отрицательное), не заключающееся в ряде (17). Мы можем представить его в виде:
k 2 = qn + k 1
где q - целое число и k 1 - любое число из ряда (17), а потому
 ,
,
т.е. значению k 2 соответствует то же значение корня, что и значению k 1, заключающемуся в ряде (17). Итак, корень n-й степени из комплексного числа имеет n различных значений.
Исключение из этого правила представляет лишь частный случай, когда подкоренное число равно нулю, т.е. r = 0. В этом случае все указанные выше значения корня равны нулю.
6.Многочлены. Деление многочленов с остатком?
Многочлен или полином (от греч. «поли» - много и лат. «номен» - имя) – класс элементарных функций классической алгебры и алгебраической геометрии. Это функция одной переменной, которая имеет вид F(x) = c_0 + c_1*x + … + c_n*x^n, где c_i – фиксированные коэффициенты, x – переменная.
Многочлены применяются во многих разделах, в том числе рассмотрении нуля, отрицательных и комплексных чисел, теории групп, колец, узлов, множеств и т.д. Использование полиномиальных вычислений значительно упрощает выражение свойств разных объектов.
Основные определения многочлена:
• Каждое слагаемое полинома называется одночленом или мономом.
• Многочлен, состоящий из двух одночленов, называют двучленом или биномом.
• Коэффициенты полинома – вещественные или комплексные числа.
• Если старший коэффициент равен 1, то многочлен называют унитарным (приведенным).
• Степени переменной в каждом одночлене – целые неотрицательные числа, максимальная степень определяет степень многочлена, а его полной степенью называется целое число, равное сумме всех степеней.
• Одночлен, соответствующий нулевой степени, называется свободным членом.
• Многочлен, все одночлены которого имеют одинаковую полную степень, называется однородным.
Определение. Пусть  и
и 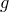 — многочлены,
— многочлены,  . Будем говорить, что
. Будем говорить, что  поделен на
поделен на 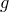 с остатком, если
с остатком, если  представлен в виде
представлен в виде  , где
, где  и
и  — многочлены, причем
— многочлены, причем  .
.
Полином  называется остатком от деления
называется остатком от деления  на
на 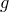 ,
,  — неполным частным.
— неполным частным.
Пример.  .
.
 .
.
Теорема. (о делении с остатком). Пусть  и
и 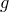 — полиномы над полем
— полиномы над полем  ,
,  . Тогда существуют единственные многочлены
. Тогда существуют единственные многочлены  и
и  над полем
над полем  такие, что
такие, что  и
и  .
.
Доказательство. Существование.
Пусть  . Положим
. Положим 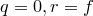 .
.
 .
.
Предположим, что теорема верна не для любого полинома  (
(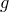 фиксируем). Среди всех многочленов
фиксируем). Среди всех многочленов  , для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его
, для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его 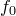 :
:
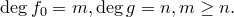
Пусть  . Положим
. Положим
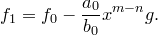
Коэффициент при  в многочлене
в многочлене  равен
равен  . Следовательно,
. Следовательно,  . Значит, для многочлена
. Значит, для многочлена  теорема верна. Существуют такие
теорема верна. Существуют такие  и
и  , что
, что  . Тогда
. Тогда
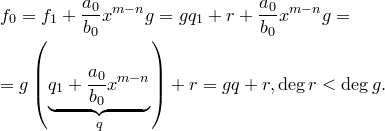
Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность. Предположим, что
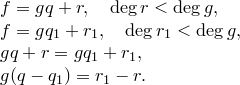
1)  . Значит,
. Значит,  ,
,
2)  .
.

Получили противоречие. Этот случай невозможен.

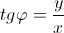
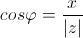
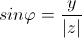
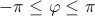 . Обозначается: arg(z).
. Обозначается: arg(z).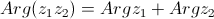
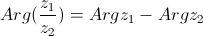
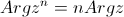
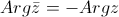
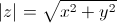
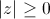 , причем |z| = 0 тогда и только тогда, когда z = 0
, причем |z| = 0 тогда и только тогда, когда z = 0
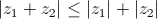 - неравенство треугольника для комплексных чисел
- неравенство треугольника для комплексных чисел


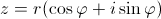
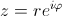






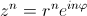

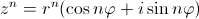
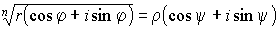
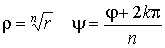
 есть арифметическое значение корня и k - любое целое число. Таким образом мы получаем:
есть арифметическое значение корня и k - любое целое число. Таким образом мы получаем:
 и
и  отличаются не кратным 2p, и будут одинаковыми, если указанные аргументы отличаются кратным 2p.
отличаются не кратным 2p, и будут одинаковыми, если указанные аргументы отличаются кратным 2p.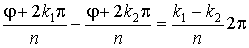
 ,
, и
и  — многочлены,
— многочлены,  . Будем говорить, что
. Будем говорить, что  , где
, где  и
и  — многочлены, причем
— многочлены, причем  .
. .
. .
. ,
,  и
и  . Положим
. Положим  .
. .
.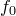 :
: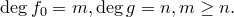
 . Положим
. Положим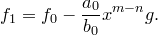
 в многочлене
в многочлене  равен
равен  . Следовательно,
. Следовательно,  . Значит, для многочлена
. Значит, для многочлена  и
и  . Тогда
. Тогда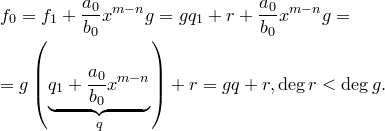
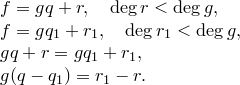
 . Значит,
. Значит,  ,
, .
.



