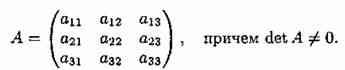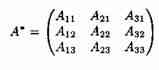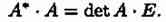Алгебраические дополнения элементов матрицы. Разложения определителя по строке.
Невырожденной матрицей называется квадратная матрица Определение. Матрицей, союзной к матрице
где Напомним, что матрица Всякая невырожденная матрица имеет обратную. Проведем доказательство для случая матрицы 3-го порядка. Пусть
Составим союзную матрицу
и инайдем произведение матриц A,A*
Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2). Аналогично убеждаемся, что
Равенства (3.2) и (3.3) перепишем в виде
Сравнивая полученные результаты с определением (3.1), получаем
|

 -го порядка, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.
-го порядка, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.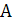 , называется матрица
, называется матрица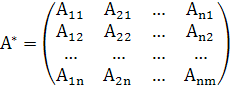 ,
,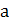 ij данной матрицы
ij данной матрицы 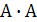 -1
-1 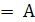 -1
-1  , где
, где  – единичная матрица того же порядка, что и матрица
– единичная матрица того же порядка, что и матрица