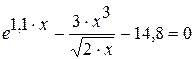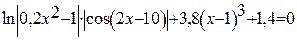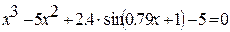Решение нелинейных уравнений

Цель: Познакомиться с приемами решения нелинейных уравнений средствами интегрированной среды MathCAD.

Задание: Решить уравнение .

Технология выполнения задания

Многие уравнения, например трансцендентные, и системы из них не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью (не более значения, заданного системной переменной TOL).

Для простейших уравнений вида f(x)=0 решение находится с помощью функции root(выражение, имя_переменной, а, b), где а,b – пределы интервала изоляции корня, которые позволяют избежать вывода корней, не представляющих интереса при решении задач, например физических.

Эта функция возвращает с заданной точностью значение переменной, при котором выражение равно нулю и реализует вычисления итерационным методом. Результаты ее использования отображены на рисунке 34.

Рисунок 34 - Пример решения уравнения с помощью функции root

Графическое решение уравнения выполняется в два этапа.

1) Необходимо преобразовать уравнение к виду f(x)=0 и построить график функции f(x);

2) Определить значение точки пересечения графика функции с осью абсцисс, используя трассировку.

Второй этап реализуется в свою очередь в несколько шагов, а именно:

a) выделим область графика функции и активизируем динамическую кнопку Масштаб , расположенную на панели инструментов Графики;

b) увеличим участок пересечения графика функции с осью ОХ, в соответствии с рисунком 35. Для этого необходимо протащить мышью по полю графика, заключив в рамку исследуемую область. При этом в окне просмотра отображаются минимальные и максимальные значения Х и У, определяющие область просмотра. Кнопки Zoom, Uzoom и FullView позволяют соответственно увеличить выделенную часть графика, снять выделение и вернуться к просмотру всего графика.

Рисунок 35 - Пример увеличения участка графика

После нажатия на кнопку Zoom, график функции принимает вид, отображенный на рисунке 36. Для получения более точного результата полученный участок пересечения графика функции с осью ОХ, важно увеличить аналогичным образом еще несколько раз. Для данного примера остановимся на участке, отображенном на рисунке 37.

c) трассировка увеличенного участка осуществляется с помощью динамической кнопки Слежение , расположенной на панели инструментов Графики. Трассировка начинает работать после выделения графика.

В окне графика появляется большое перекрестие из двух черных пунктирных линий. С помощью указателя мыши его можно перемещать по графику с дискретностью, определяемой заданным шагом изменения абсциссы х. При этом координаты текущей точки ближайшей кривой графика, на которую установлено перекрестие, отображаются в окне трассировки, изображенном на рисунке 38.

Это позволяет в приближении выявить координаты особых точек графика, в данном случае решение уравнения f(x)=0.

Кнопки Copy X и Copy Y позволяют занести соответствующие координаты в буфер обмена. Кнопка Close завершает трассировку и закрывает окно трассировки. Если установлен флажок Trace Data Point, то при трассировке указатель автоматически устанавливается на точку ближайшей кривой, отслеживая ее ход. При снятом флажке указатель может быть установлен в любую точку области графика, при этом координаты этой точки отображаются в окне трассировки.

Рисунок 36 - Участок графика после первого увеличения

Рисунок 37 - Участок графика после многократного увеличения

В нашем случае при трассировке получаем результат, отображенный на рисунке 38.

Рисунок 38 - Трассировка увеличенного участка графика

Таким образом, при решении трансцендентного уравнения первым способом, то есть с помощью встроенной функции Root, получено решение х=1,592, а графическим способом получен результат х=1,5924.

Для поиска всех корней обычного полинома p(x) степени n MathCAD поддерживает функцию polyroots(V), которая возвращает вектор всех корней полинома степени n, коэффициенты которого находятся в векторе V, имеющем длину n+1.

Замечание: Не рекомендуется использовать эту функцию, если степень полинома выше пятой-шестой, так как трудно получить малую погрешность вычисления корней.

Таблица 17 - Индивидуальные варианты лабораторной работы №15

№ В	Варианты индивидуальных заданий
Решить уравнение f(x)=0 одним из предложенных преподавателем способом

 

Продолжение таблицы 17