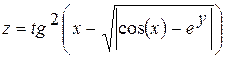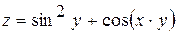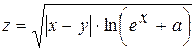Построение графика функции

Цель: Освоить построение двумерных и трехмерных графиков функций, научиться представлять значения функции для заданного диапазона значений аргументов в табличном виде.

Задание:

a) Построить график функции у=sin(x);

b) Построить график функции z=cos(0,2xy) и получить таблицу ее значений для заданных аргументов.

Технология выполнения задания

MathCAD позволяет строить самые разнообразные графики:

- в декартовой и в полярной системе координат;

- с масштабной сеткой и без неё;

- с линейным и логарифмическим масштабом;

- с отметкой линий прямоугольниками, крестами, ромбами и т.д.

Для визуального отображения различных зависимостей используют семь видов графиков. Типов графиков в MathCAD, конечно, намного больше, но на панели инструментов имеется ровно семь кнопок для создания семи типов графиков.

Самый распространенный график: двухмерный декартов график (X-Y Plot), иллюстрирующий связи между двумя или несколькими векторами.

 

Алгоритм построения двумерного декартова графика

Декартов график строится, как правило, в два шага:

a) задание вида функций одной переменной, например f(x):=sin(x);

b) построение графика.

1) Рисование на экране дисплея заготовки графика - прямоугольника с чёрными квадратиками у левой и правой сторон. В соответствии с рисунком 27, заготовка графика появляется в отмеченном курсором месте после того, как пользователь нажмёт одну из семи кнопок панели инструментов “Графики”, в данном случае , рассмотренную выше на рисунке 24.

Рисунок 27 - Шаблон для построения двумерного графика

2) Заполнение пользователем двух чёрных квадратиков заготовки графика именем функции и именем аргумента. Если функций больше одной, то их имена вводятся через запятую. В заготовке есть и другие чёрные квадратики, которые можно не заполнять. Среда MathCAD заполнит их сама.

График появляется на дисплее после вывода курсора из зоны графика (автоматический режим расчётов) или после нажатия клавиши F9 (ручной или автоматический режим расчётов). Параметры графика задаются стандартами по умолчанию, в соответствии с рисунком 28.

 

Рисунок 28 - Автоматически построенный график

Рисунок 29 - Вид графика функции после форматирования

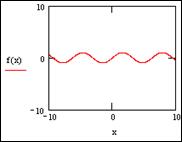
3) Этот этап необходим, если параметры графика, установленные по умолчанию, не устраивают пользователя, и он хочет их изменить.

Для этого достаточно щелкнуть по изменяемому параметру и ввести новое числовое значение. Например, изменим значения –1 и 1 на –10 и 10 соответственно, получим следующий вид графика, представленного на рисунке 29 той же самой функции одной переменной.

Если аргумент представляет собой угол, изменяющийся от 0 до 360 градусов, то целесообразно использовать полярный график(Polar Plot).

Графически отобразить функцию двух аргументов можно с помощью графика поверхности(Surface Plot).

Методы построения графика поверхности

1) Упрощенный метод построения поверхности.

Упрощенный метод построения поверхности, изображенный на рисунке 30, аналогичен построению двумерного графика, а именно:

- задается функция двух переменных, например f(x,y):=cos(0.2xy);

- определяется место вставки графика и на панели инструментов Построение графика выбирается кнопка ;

- в нижнем левом углу задается имя функции, в данном случае f.

Недостатком этого метода построения поверхности является неопределенность в масштабировании, поэтому для получения приемлемого вида графика требуется форматирование.

Рисунок 30 - Построение графика поверхности упрощенным способом

2) Применение мастера построения трехмерных графиков.

При использовании данного способа необходимо, как и в предыдущих способах, сначала задать функцию и выбрать место вставки графика, затем в пункте меню Вставка выбрать команду График – Мастер 3-d участка и в диалоговом режиме установить необходимые параметры.

3) Применение встроенной функции.

Применение встроенной функции GreateMesh(F, s0, s1, t0, t1, sgrid, tgrid, fmap). Эта функция возвращает массив из трех матриц, представляющих координаты x, y, z для функции F, определенной в векторной параметрической форме в качестве функции двух переменных sgrid и tgrid. Аргумент fmap – трехэлементный вектор значений, задающий число линий в сетке изображаемой функции. Построение графика функции с помощью данной функции проиллюстрировано на рисунке 31.

Рисунок 31 - Построение графика поверхности с помощью

встроенной функции

Очень часто, особенно при поиске оптимумов функции двух переменных, полезнее просмотреть не график поверхности, а карту линии уровня, которые подобны линиям на физической географической карте, охватывающим горы и впадины (минимумы и максимумы).

На место линий графика можно поставить маленькие стрелочки, отмечающие направление изменения функций двух переменных. Тогда получится векторное поле (Vector Field Plot).

Гибридом декартова графика и графика поверхности является так называемый трёхмерный точечный график (3D Scatter Plot). Его главное отличие от графиков, отображающих прямоугольные матрицы, в том, что с его помощью можно изобразить взаимосвязь трёх векторов.

Графики можно расцветить так, чтобы более высокие зоны имели тёплые цвета, а более низкие – холодные. Пакет MathCAD может раскрасить объёмные конструкции так, чтобы пользователь смог увидеть всё, что ему нужно.

Основной недостаток трёхмерной графики MathCAD и других подобных пакетов – в том, что область изменения аргументов должна быть прямоугольной.

Для выполнения второй части задания необходимо воспользоваться понятием ранжированной переменной.

 

Таблица 14 - Индивидуальные варианты лабораторной работы №12

№ В	Варианты индивидуальных заданий
Построить график функции z=f(x,y), где a, b - некоторые константы (задать самостоятельно)

Продолжение таблицы 14