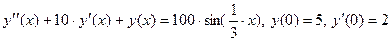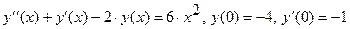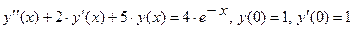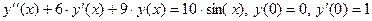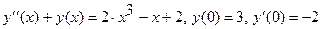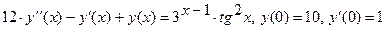Решение дифференциальных уравнений
Цель: Изучить специальные функции, позволяющие осуществлять решение обыкновенных дифференциальных уравнений средствами интегрированной среды. Задание: Найти частное решение дифференциального уравнения второго порядка Технология выполнения задания Многие серьезные физические и научно-технические задачи (особенно относящиеся к анализу динамических систем и к их математическому моделированию) базируются на решении систем дифференциальных уравнений. Нелинейные дифференциальные уравнения и системы с такими уравнениями, как правило, не имеют аналитических методов решения. Поэтому особенно важна возможность их решения численными методами и желательно представление решений в графическом виде. Решение дифференциальных уравнений в интегрированной среде MathCAD осуществляется с помощью специальной функции odesolve(x, b[, step]). Эта функция возвращает решение дифференциальных уравнений, описанных в блоке Given, при заданных начальных условиях и конце интервала интегрирования b. Ее можно активизировать, используя кнопку Мастера функций Функция имеет некоторые особенности. Например, если указано число шагов step, то решение выполняется с фиксированным шагом, иначе – адаптивным методом. Хотя аналитическое выражение для этой функции не выводится, но графическое ее представление не вызывает затруднений, кроме того с ней можно выполнять математические преобразования. Решение дифференциального уравнения второго порядка, указанного в задании, изображено на рисунке 40. Дифференциальные уравнения могут быть записаны с использованием шаблонов, которые можно активизировать с помощью динамических кнопок Рассмотренная функция, для решения дифференциального уравнения, использует фиксированный шаг метода Рунге-Кутта. Для использования адаптивного метода необходимо щелкнуть правой клавишей мыши по функции odesolve и выбрать в ниспадающем меню Adaptive. Для решения систем обыкновенных дифференциальных уравнений в среде MathCAD они должны быть представлены в форме Коши, то есть:
Эти системы можно представить в векторной форме: Y(x0)=Y0 и Y′=F(x, Y). Тогда решение системы обыкновенных дифференциальных уравнений в форме Коши осуществляется аналогично решению одиночного дифференциального уравнения, но должно быть организовано в векторной форме. При этом добавление каждый раз очередного уравнения увеличивает число уравнений в их векторной записи. Интегрированная среда MathCAD 2000 PRO помогает решать задачи такого класса с помощью ряда (около десятка) встроенных функций, одна из которых функция rkfixed(y, x1, x2, n, F). Эта функция возвращает матрицу решений методом Рунге-Кутта системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F на интервале от х1 до х2 при фиксированном числе шагов n. Однако более точный результат можно получать, используя функцию Rkadapt, так как она позволяет автоматически изменять шаг, то есть она более привлекательна для решения систем дифференциальных уравнений, имеющих относительно медленно изменяющиеся решения.
Рисунок 40 - Пример решения дифференциального уравнения Таблица 19 - Индивидуальные варианты лабораторной работы №17
Продолжение таблицы 19
Продолжение таблицы 19
|

 , удовлетворяющего начальным условиям y(1)=0, y′(1)=3.
, удовлетворяющего начальным условиям y(1)=0, y′(1)=3. на панели инструментов Стандартная.
на панели инструментов Стандартная. и
и  , расположенных на панели инструментов Калькулус или в виде
, расположенных на панели инструментов Калькулус или в виде 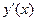 , где «′» задается при помощи комбинации клавиш Ctrl + F7.
, где «′» задается при помощи комбинации клавиш Ctrl + F7.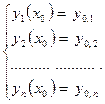 - задает начальные условия,
- задает начальные условия,  - система ОДУ.
- система ОДУ.