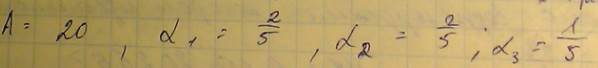Способы нормализации локальных критериев
Проблема нормализации локальных критериев возникает каждый раз когда решаются задачи, в которых локальные критерии имеют различную размерность. Например, для космических кораблей важным критерием является масса, другим стоимость. Сравнивать критерии массы и стоимости сравнивать невозможно. В связи с этим необходимо уметь нормализовать критерии. По существу нормализация не требуется только при использовании способа относительной уступки, так как в этом случае нормализация осуществляется путем деления на максимальное значение столбца. В общем случае каждое новое значение критерия получают путем деления текущего iого значения критерия на общее идеальное значение этого критерия
На данным момент не существует лучшего метода для определения идеального вектора. Все рассмотренные способы характерны для случая, кода все рассмотренные локальные критерии имеют одинаковую важность. А в большинстве практических задач локальные критерии имеют неодинаковую важность. В связи с этим разработан и используется ряд способов принятия решений ыв условиях когда локальные критерии имеют неодинаковую важность. Основными подходами в решении таких задач является использование:
Ряд приоритетов принято Если среди критериев имеется несколько с одинаковой важностью, то ряд может быть записан следующим образом: Вектор приоритетов Весовой вектор
Если критериев всего 3, то значения этого критерия могут вычисляться через значения Для отдела центрального конструкторского бюро необходимо преобрести устройство вывода документации на печать (плоттеры). Предварительным анализом поставщиков установлено, что могут быть закуплены плоттеры 3х моделей
Fмм - максимально возможный формат отпечатанного чертежа Rdpi - Vкб - объем буффера Требуется используя рассмотренные способы компромисса определить лучший вариант плоттера в двух условиях:
Решение:
В качестве идеального вектора выберем: Ug=<10,20,256> Тогда учитывая, что всего критериев 3 воспользуемся для вычисления формулами
2.1 принцип равномерности – по принципу квазиравенства 2, по максимину 3ий вариант 2.2 принцип уступки: a) абсолютная уступка – 3 вариант b) относительная – 3ий вариант 2.3 Выделение одного оптимизирующего критерия - для плоттера из выбранных критериев наиболее важным является первый, поэтому по таблице 2 выбираем максимальный элемент в столбце F, следовательно поэтому критерию выбираем строку 3. 2.4 Принцип последовательной уступки. Выбрали первый столбец, максимальное значение 1. Уступка 0.5. 1-0.5=0.5. Значит вычеркиваем значение <0.5. Отбросили первую строку. По первому столбцу отобрали. Теперь отбираем по второму, максимальное значение 0,7. Уступка 0,05. 0,7-0,05=0,65. Вычеркиваем строку со значеним в столбце <0.65.
Выберев в качестве вектора приоритетов вектор, имеющий вид
Таже последовательность действий По квазиравенству 3, макисмимина 2 По абсолютной уступке 2 По относительной 2 Выделение одного оптимизирующего критерия 2 Последовательная уступка 2
|

 Принципиально сложным является выбор идеального вектора. Для формализации выбора такого вектора используются 3 способа:
Принципиально сложным является выбор идеального вектора. Для формализации выбора такого вектора используются 3 способа: и в ряде приоритетов принято считать что вариант записанный левее текущего является более приоритетным.
и в ряде приоритетов принято считать что вариант записанный левее текущего является более приоритетным.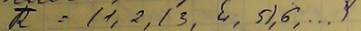 что означает что критерий 3,4,5 имеют одинаковы приоритет, а по важности располагаются на 3ем месте после критериев 1,2. Такая запись получила название жесткого приоритета, так как непосредственно в этой записи указывается собственно приоритет критерия.
что означает что критерий 3,4,5 имеют одинаковы приоритет, а по важности располагаются на 3ем месте после критериев 1,2. Такая запись получила название жесткого приоритета, так как непосредственно в этой записи указывается собственно приоритет критерия.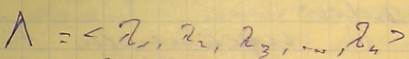 - это способ косвенного задания приоритетов. Компоненты этого вектора определяют степень относительного превосходства двух соседних критериев из ряда приоритетов. То есть лямбдаi показывает во сколько раз критерий Fi важнее критерия Fi+1.
- это способ косвенного задания приоритетов. Компоненты этого вектора определяют степень относительного превосходства двух соседних критериев из ряда приоритетов. То есть лямбдаi показывает во сколько раз критерий Fi важнее критерия Fi+1.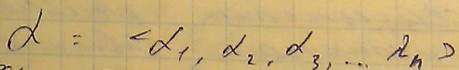 - представляет собой n мерный вектор, элементы которого связаны следующими соотношениями:
- представляет собой n мерный вектор, элементы которого связаны следующими соотношениями: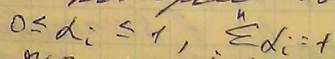
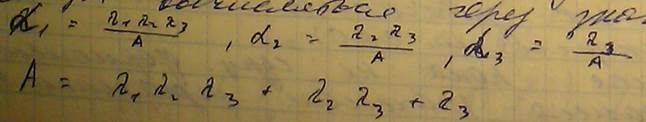 Пример многокритериальной задачи принятия решения
Пример многокритериальной задачи принятия решения Перейдем от таблицы 1 к таблице 2, путем приведения значений элементов исходной таблицы:
Перейдем от таблицы 1 к таблице 2, путем приведения значений элементов исходной таблицы: