Различают шкалы отношений, шкалы интервалов и шкалы отсчета.
Рассмотренный пример с отношением во сколько раз или на сколько раз представляет собой шкалу отношений. Если к шкале отношений вводящей множитель k добавить l определяющий начало координат отношений переходит к шкале интервалов. Конкретное значение коэффициента k и коэффициента l и определяет то значение интервала критерия эффектиности K, которое может быть использовано в теории принятия решений. Примером такого критерия является дата выпуска изделия. Принято считать чем меньше множество допустимых преобразований D, тем шкала более совершенна. Из всех совершенных шкал наиболее совершенной является абсолютная шкала. Для которой единственным допустимым преобразованием является тождественное преобрзование. Абсолютные шкалы позволяют измерять количество объектов. По абсолютной шкале можно говорить о количестве отличников учебы в группе и тем самым сравнивать, с другой группой. Абсолютные шкалы могут получить критерии образованные путем преобразований исходных критериев, шкалы которых менее совершенны. Например, если k – критерий отношения, то если этот критерий отнести к некоторому эталонному значению k, то можно получить абсолютную шкалу этого критерия. В соответствии с таким определением говорят, что абсолютные шкалы всегда относятся к количественным. К количественным можно отнести все шкалы более совершенные, чем шкалы интервалов. В большинстве случаев количественные критерии позволяют давать объективные оценки проектируемого изделия, но иногда можно говорить о субъективных оценках. Например о субъективных оценках экспертов о качестве внешнего вида изделия. Особенно принципиально удобство работы на аппаратуре. К таким критериям относятся все критерии, которые не представляется возможным измерить с помощью физических приборов. На ряду с абсолютной шкалой отношений и интервалов существуют номильная, классификационная и порядковая. Номинальная характеризуется тем, что соответствующее множество допустимых преобразований состоит только из взаимно однозначных функций. Считается, что номинальная шкала – наименее совершенная шкала и применяется самый слабый вид измерений, указывается только одинаковы или нет 2 объекта по одному и тому же признаку. Признаки используемые в номинально шкале применяются часто(анкетные данные). Порядковая шкала – для нее множество всех допустимых функций состоит из множества монотонно возрастающих функций. Считается, что чем точнее охарактеризованы и оценены возможные значения эталонов, тем меньше разброс в оценках и тем оценки надежней. Например, бальные оценки могут субъективно отражать качества объекта. Когда отражают такие принципы, говорят что они измерены в порядковой шкале. Обощая рассмотренный материал отметим, что все критерии эффективности могут иметь различные типы шкал. Все критерии, имеющие интервальную и более совершенные шкалы называются количественными. Критерии, имеющие порядковую шкалу могуть быть только качественными. Таблица шкал.
Тип шкалы критерия необходимо учитывать во всех случаях решения вопросов о том, какие действия или операции следует производить при выполнении оценок тех или иных критериев утверждение об измерениях или оценках называется осмысленным, если его истинность не изменится. Имеет смысл сравнивать средние значения оценок, если они получены в интервальной шкале
Одним из таких методов является метод попарных сравнений Саати. В настоящее время при решении целого ряда инженерных задач приходится приписывать различным объектам коэффициенты важности. При оценке степени поражения информации хранящейся в массивах на объектах необходимо сопоставить этой информации некоторые коэффициенты важности. Тогда можно говорить о нанесении противникам или злоумышленником некоторого ущерба тому или иному массиву, оцениваемому в данном случае с помощью критерия эффективности, который называется вероятный ущерб, рассчитываемый по выражению Wi=Ci*Pi Pi – вероятность преодоления злоумышленником всей системы преград к массиву i для того, чтобы сопоставить каждому массиву его коэффициент важности воспользуемся методом Саати. Так как он является одним из наиболее простых и позволяет оперативно решать задачи определения важности, наделяя их некачественными, а количественными значениями. В соответствии с этим методом результаты попарного сравнения различных параметров описываются отношениями их весов, которые представляются в виде матрицы отношений или матрицы Саати.
Саати доказал справедливость равенства: (А-nE)k=0 * Где лямбдаi и лямбда j интенсивность относительной важности хранимой информации, а k – искомый вектор весов E – единичная матрица. Из уравнения(*) найдем значение вектора k. Обозначим сомножетели в скобках как матрицу A*. Для вычисления вектора весов необходимо рассчитать, т.е решить уравнение звездочка. Саати доказал, что матрица весов(А) имеент ранг равный 1. При этом n – единственное собстенное число этой матрицы следовательно уравнение * имеет единственное ненулевое решение, такое что
Пример Хранится 5 массивов информации, интенсивности относительной важности попарных сравнений в виде шкалы относительной важности представлены таблицой из двух столбцов
Определить коэффициенты важности информации хранящейся в массиве. Для получения исходных данных методом экспертного опроса сотрудников айтиотдела предприятия составлена матрица попарных сравнений – матрица Саати А=
А*=(A-nE)=0 Матричное уравнение * имеет единственное нетривиальное решение, тогда и только тогда, когда определитель матрицы А*=0. В соответствии с известной математикой эта матрица А* примет вид. А*=
Для решения уравнения * воспользуемся ппп маткад, которое позволит получить решение в виде: Выберем наибольшее значение - N5 подставим в матрицу А* вместо n.
Вычислив значения элементов матрицы и округлив их до сотых
Умножим полученную матрицу на вектор коэффициентов К. К=
Получим:
Полученное уравнение всегда будет иметь нулевое решение. Заменим одно из уравнений системы на уравнение нормировки: K1+k2+k3+k4+k5=1 K=<k1,k2,k3,k4,k5>=<0.508 0.255 0.136 0.071 0.03> Максимальное значение будет составлять 9,1% N1=508 N2=255 N3=136 N4=71 N5=30
|
На приктике пользуются только осмысленными преобразованиями, т.е. при которых не изменяется результат ранжирования. Для того чтобы такие преобразования не влияли на качество сравнения двух и более объектов применяют специальные методы, как правило попарных сравнений.
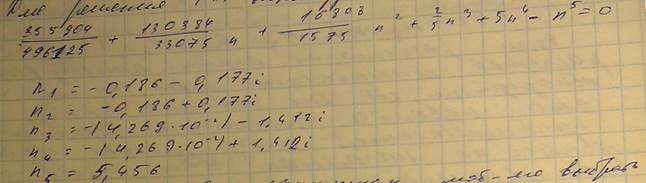
Если рассчитать относительную ошибку вторых расчетов относительно первых, то обнаружим, что она составляет 23%, что позволяет говорить о том, что данный приблизительный метод может использоваться на начальном этапе проектирования, который должен быть обязательно уточнен например методом попарных сравнений Саати.
