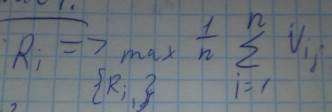Принятие решений с использованием критерия Лапласа
Этот критерий базируется на принцип недостаточного основания, которой тоже принадлежит Лапласу. В соответствии с этим критерием вероятности того, что природа создающая неопределенность находится в n состояниях вероятности, которых равны между собой. Тогда такие вероятности берут из выражений qi=1/n. N число возможных состояний природы. Для того чтобы получить приемлимое решение в условиях неопределнности необходимо:
Необходимо выбрать такую стратегию
Пример. Транспортное предприятие должно решить вопрос так, чтобы удовлетворить спрос всех клиентов и получить при этом наименьший экономический проигрыш. Выигрыш или проигрыш автотранспортного предприятия заключается:
Необходимо обосновано выбрать стратегию развития предприятия. Предприятию неизвестно точно какие перевозки оно будет осуществлять. Известно только, что прогноз этих перевозок составляет 10,15,20,25 тысяч тонн. Так как в данном случае идет речь о стоимости перевозок, которая для автопредприятия должна быть минимальна, необходимо критерий лапласса записать в виде:
Тогда можно отметить, что варианты спроса – состояния «природы», а варианты развития предприятий – стратегии, котороые может выбрать предприятие. В соответствии с критерием Лапласса вероятность событий qi=0.25. Тогда в результате выбора стратегий R1 получим: R1=>0.25(12+6+20+24)=15,5 R2=>0.25*53=13.25 R3=>0.25*(23+18+15+19)=18.75 R4=>21.75 R2 Наименьшее и в соответствии с критерием Лапласса лучшей является стратегия R2.
Решим считая, что нам известна матрица рисков rji= R1=0.25*(5++0+11+9)=6.25 R2=0.25*(0+0+3+13)=4 R3=0.25*(17+11+6+4)=9.5 R4=0.25*(21+17+12+0)=12.5
|