Плоскі і сферичні дзеркала
Побудова зображення в плоскому дзеркалі базується на використанні закону відбивання світла. Нехай над плоским дзеркалом знаходиться точкове джерело світла S, що освітлює це дзеркало (2).
Рис. 2. Рис. 3.
Із всього світлового потоку виберемо два промені 1 і 2, які падають на дзеркала під різними кутами - Зображення, яке отримується за рахунок перетину не самих променів, а їх продовжень, називають уявним. Така назва пов'язана з тим що в точку Отже, в плоскому дзеркалі отримується уявне зображення світлової точки S, яке розміщено симетрично їй відносно дзеркала в точці S1. Геометрична оптика вивчає прийоми побудови зображень різних джерел і розрахунки оптичних пристроїв і приладів, які призначені переважно для перетворення світлових променів. Одним із таких приладів є сферичне дзеркало. Введемо позначення: P - полюс дзеркала (вершина сферичного сегмента); О — центр сфери, або центр кривизни (геометричний центр сферичної поверхні радіуса R); PO – головна оптична вісь дзеркала (нормаль до дзеркала, яка проходить через полюс і центр сфери) (рис.3). Виведемо формулу сферичного дзеркала. Точкове джерело світла знаходиться на головній оптичній осі вгнутого сферичного дзеркала (рисунок 3) на відстані d = PS від полюса. Зображення буде в точці S1 ( Позначимо: Виділимо паралельно до головної оптичної осі вузький (параксіальний) пучок променів. Кути
Оскільки
Формула (7) справедлива і для вгнутого, і для опуклого дзеркала. Промені, що падають на дзеркало до головної оптичної осі, після відбиття збираються в одній точці, яка називається головним фокусом F сферичного дзеркала. Знайдемо відстань від головного фокуса до полюса дзеркала P. Ця відстань називається головною фокусною відстанню і позначається буквою F. Нехай джерело світла знаходиться на нескінченності ( У цьому випадку
Поверхня, яка проведена через точку F і перпендикулярна до головної оптичної осі, називається фокальною площиною. Вона є геометричним місцем нескінченної множини фокусів.
|



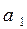 і
і  . Після відбивання від дзеркала ці промені розходяться. Продовжені промені перетинаються в точці
. Після відбивання від дзеркала ці промені розходяться. Продовжені промені перетинаються в точці  , яка знаходиться по інший бік дзеркала. Якщо будемо дивитися на дзеркало, то нам здаватиметься, що промені 1 і 2 виходять із цієї точки, неначе там знаходиться джерело світла. Відповідно точка
, яка знаходиться по інший бік дзеркала. Якщо будемо дивитися на дзеркало, то нам здаватиметься, що промені 1 і 2 виходять із цієї точки, неначе там знаходиться джерело світла. Відповідно точка  , де бачимо світлову точку, не потрапляє світлова енергія. Якщо в точку S1 помістити екран, то на ньому не буде зображення точки S. Це характерна властивість уявного зображення.
, де бачимо світлову точку, не потрапляє світлова енергія. Якщо в точку S1 помістити екран, то на ньому не буде зображення точки S. Це характерна властивість уявного зображення. - відстань від полюса до зображення).
- відстань від полюса до зображення).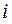 - кут падіння променя SB до головної оптичної осі; r - кут нахилу від відбитого променя до головної оптичної осі;
- кут падіння променя SB до головної оптичної осі; r - кут нахилу від відбитого променя до головної оптичної осі;  - кут нахилу осі BC. Нехай BD = h. Кут γ є зовнішнім до трикутника BOS, тому
- кут нахилу осі BC. Нехай BD = h. Кут γ є зовнішнім до трикутника BOS, тому  . Аналогічно,
. Аналогічно,  . Тоді
. Тоді  .
. досить малі, тому синуси можна замінити кутами, а довжиною відрізка PD знехтувати. Тоді
досить малі, тому синуси можна замінити кутами, а довжиною відрізка PD знехтувати. Тоді
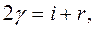 то підставивши вирази для кутів
то підставивши вирази для кутів  отримаємо
отримаємо (7)
(7) ).
). Отже,
Отже, (8)
(8)


