Аппроксимация криволинейных участков профиля резца

Профили обрабатываемых деталей состоят (по заданию) из прямолинейных, конических и дуговых участков. Соответствующие коническим и дуговым участкам детали, участки профиля фасонного резца будут несколько отличатся от них, что вызывает необходимость замены плоских кривых дугами других окружностей или другими прямыми.

Конический участок на резце аппроксимируется прямой линией с углом (рис. 8 а):

,

где h_max, h_min – глубины профиля для крайних точек конического участка;

l_к – длина конического участка.

Отклонение D f фактической формы конического участка детали от теоретической в средней точке С этого участка (рис. 8 б):

,

где h_Сф – глубина профиля резца в средней точке, полученная при профилировании;

h_Ст – глубина профиля резца в средней точке, полученная на заменя-ющей прямой.

Рис. 8

Отклонение D f не должно превышать допуск на соответствующий размер профиля детали. В противном случае конический участок заменяют двумя коническими участками.

Расчетная кривая для обработки дугового участка детали заменяется одной или несколькими дугами окружностей в зависимости от требуемой точности. Для определения радиуса заменяющей окружности используют координаты трех точек расчетной кривой А, Б, В (рис. 9). Корригированный радиус r_x в профильной плоскости резца для дугового участка детали с радиусом r определяют по формуле:

где l_r – ширина дугового участка;

f_r = h_Б - h_А – глубина дугового участка в профильной плоскости резца.

Заметим, что формула справедлива и для несимметричных дуговых участков, т.е. когда участки АБ или БВ отсутствуют.

Погрешность от замены криволинейного участка профиля дугой окружности по нормали к ней находят по формуле:

,

где x_n, y_n – координаты точки n, наиболее удаленной от дуги окружности;

x₀, y₀ – координаты центра заменяющей окружности.

Рис. 9

Величина D r не должна превышать 0,75 допуска на данном участке профиля. В противном случае расчетную кривую следует заменять дугами двух и более окружностей.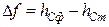