Задание. Не забудьте, что выполнение всех последующих заданий должно начинаться с текстовой строки, содержащей «Задание №»
Не забудьте, что выполнение всех последующих заданий должно начинаться с текстовой строки, содержащей «Задание №», где № – номер задания. Также помните, что для правильности вычислений перед выполнением каждого пункта задания следует выполнять команду restart. Перед выполнением контрольных заданий следует набирать в текстовом режиме «Контрольные задания». Эти правила оформления относятся ко всем работам. 1. Запустите Maple. Переведите первую строку в текстовую и наберите в ней: «Практическая работа №2». Нажмите Enter. Строкой ниже наберите: «Выполнил студент...» и свою фамилию, а на следующей строке наберите: «Задание №1». 2. Определите функцию > f:=sqrt(1-x^2-y^2);
> f:=subs({x=rho*cos(phi),y=rho*sin(phi)},f);
> f:=simplify(%);
3. Определите функцию > f:=piecewise(x<-1, x, -1<=x and x<1, -x^2, x>=1, -x);
> %+x: simplify(%);
4. Перейдите в текстовый режим и наберите «Задание №2». После не забудьте перейти в режим командной строки. 5. Дано число а =57/13. Найти его целую часть x и дробную часть y и убедиться, что a = x + y. Наберите: > a:=57/13: > y:=frac(a);
> x:=trunc(a); > x+y;
6. Дано комплексное число В командной строке наберите: > z:=(2-3*I)/(1+4*I)+I^6: > Re(z); Im(z);
> w:=conjugate(z);
> z+w;
7. Перейдите в текстовый режим и наберите «Задание №3». После не забудьте перейти в режим командной строки. 8. Найти все решения системы уравнений Наберите: > eq:={x^2-y^2=1,x^2+x*y=2}; > _EnvExplicit:=true: > s:=solve(eq,{x,y});
Теперь найдите сумму двух наборов решений. Наберите: > x1:=subs(s[1],x): y1:=subs(s[1],y): x2:=subs(s[2],x): y2:=subs(s[2],y): > x1+x2; y1+y2; Чему равны эти суммы решений? 9. Численно решите уравнение > x=fsolve(x^2=cos(x),x); x =.8241323123 10. Перейдите в текстовый режим и наберите «Задание №4». После не забудьте перейти в режим командной строки. 11. Построить график > plot(sin(x)/x, x=-4*Pi..4*Pi, labels=[x,y], labelfont=[TIMES,ITALIC,12], thickness=2);
12. Построить два графика на одном рисунке: график функции > plot([ln(3*x-1), 3*x/2-ln(2)], x=0..6, scaling=CONSTRAINED, color=[violet,gold], linestyle=[1,2], thickness=[3,2]);
13. Построить область, ограниченную линиями: > with(plots): > inequal({x+y>0, x-y<=1, y=2}, x=-3..3, y=-3..3, optionsfeasible=(color=red), optionsopen=(color=blue,thickness=2), optionsclosed=(color=green, thickness=3), optionsexcluded=(color=yellow));
|

 и перейдите в ней к полярным координатам
и перейдите в ней к полярным координатам  ,
,  . Упростите полученное выражение. Для этого наберите:
. Упростите полученное выражение. Для этого наберите: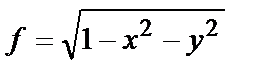
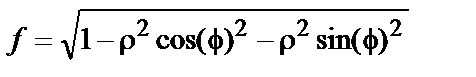

 и прибавьте к ней х. Для этого наберите:
и прибавьте к ней х. Для этого наберите:



 . Найти его вещественную и мнимую части, а затем комплексно сопряженное ему число w и убедиться, что w+z= 2Re(z).
. Найти его вещественную и мнимую части, а затем комплексно сопряженное ему число w и убедиться, что w+z= 2Re(z).
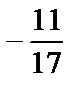



 ,
, 
 . Наберите:
. Наберите: жирной линией в интервале от -4p до 4p. Наберите:
жирной линией в интервале от -4p до 4p. Наберите:
 и касательную к нему
и касательную к нему  . Наберите:
. Наберите:
 ,
, 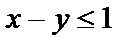 ,
,  .
.



