В) эквивалентная система с главным вектором и главным моментом
Далее заменяем (векторным суммированием) сходящиеся в точке О векторы сил
которую называют главным вектором системы сил. Геометрически складываем также все векторы моментов пар сил
который называют главным моментом системы сил. Таким образом, произвольную систему сил, действующих на тело, мы эквивалентно заменили двумя силовыми факторами: главным вектором Следует отметить, что при параллельном переносе сил
R= Таким образом, главный вектор системы сил можно определить геометрически с помощью многоугольника сил. Аналитически главный вектор определяется тремя своими проекциями на координатные оси; R R R
Главным моментом Мо системы сил F1: F2,..., Fn относительно точки называется векторная сумма моментов этих сил относительно этой точки, т. е M Таким образом, главный момент системы сил относительно точки можно определить геометрически с помощью многоугольника моментов этих сил относительно данной точки. Аналитически главный момент относительно точки определяется тремя своими проекциями на координатные оси:
M M M или
Заметим, что понятия главного вектора и равнодействующей системы сил не тождественны. Как мы увидим в следующей главе, не всякая система сил имеет равнодействующую. Если же система сил и приводится к равнодействующей, то последняя, хотя геометрически и равна главному вектору, но имеет вполне определенную линию действия, в то время как главный вектор (также и главный момент) является свободным вектором.
|

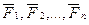 одной силой
одной силой ,
, , заменяя их одним (равнодействующим) моментом
, заменяя их одним (равнодействующим) моментом ,
, и главным моментом
и главным моментом  ,см. рисунок 19,в.
,см. рисунок 19,в. в любой центр приведения не изменяются ни величины, ни направления этих сил. Поэтому главный вектор
в любой центр приведения не изменяются ни величины, ни направления этих сил. Поэтому главный вектор  системы сил не является ее инвариантом, т. к. он зависит от выбранного центра приведения. При перемене центра приведения изменяются и моменты сил системы относительно этого центра, поэтому изменяется и главный момент.
системы сил не является ее инвариантом, т. к. он зависит от выбранного центра приведения. При перемене центра приведения изменяются и моменты сил системы относительно этого центра, поэтому изменяется и главный момент.







 ;
;  ;
; 



