ДИНАМИКА
· 1.Динамика изучает движение материальных тел под действием приложенных к ним сил.1) Ма́сса (от др.-греч. μάζα, кусок теста) — скалярная физическая величина, одна из важнейших величин в физике. Масса (инертная масса) — физическая величина, характеризующая меру инертности тела Единица массы — килограмм (кг).2) Мат.точкой называется материальное тело размерами которого при изучении данного движения можно пренебречь.3) Система материальных точек – это модель, являющаяся совокупностью нескольких материальных точек (2-х и больше) Расстояние между точками является конечным. Каждая МТ в такой СМТ моделирует частицу тела. Абсолютно твердое тело (АТТ) – это такая СМТ, взаимное расположение которых не меняется, или сплошное тело, форма и размеры которого не изменяются.4) Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений. 5) 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
где
В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5]. Второй закона Ньютона можно также сформулировать с использованием понятия импульса: В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе[6].
где · 3-й: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса. 6) Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятс. 2. 1)Согласно основному закону динамики имеем:
Проектируя обе части равенства на оси декартовой системы координат и учитывая, что
или
Так как действующие на точку силы зависят от времени, от положения точки (координат точки) и от скорости, то правая часть уравнений может быть функцией этих переменных. Решение второй задачи динамики сводится к тому, чтобы из данных уравнений, зная силы, найти закон движения точки. Для этого необходимо проинтегрировать соответствующие дифференциальные уравнения. При интегрировании каждого дифференциального уравнения в полученное решение входят две постоянных интегрирования С1 и С2. Для определения значения этих постоянных используют, так называемые, начальные условия. За начальный момент времени обычно принимают t=0. Положение, которое занимает точка в момент t=0, называют начальным положением Таким образом, для решения второй задачи динамики, кроме действующих сил, необходимо знать начальные условия. Решение второй задачи динамики точки с помощью интегрирования дифференциальных уравнений движения сводится к следующим операциям: составление дифференциальных уравнений движения. В случае прямолинейного движения необходимо: выбрать начало отсчета (как правило, его совмещают с начальным положением точки); координатную ось направляют в сторону движения; изобразить движущуюся точку в произвольном положении ( записать дифференциальное уравнение движения точки, спроектировав все силы на ось координат. Способы интегрирования дифференциального уравнения движения известны из курса высшей математики и зависят от вида правой части уравнения. Если при решении задачи необходимо искать зависимость скорости от координаты x), уравнение преобразуют к переменному x. Для этого
и дифференциальное уравнение примет вид
Определение постоянных интегрирования производится из начальных условий, которые следует установить из условия задачи. 2) 4. Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трёхгранника. Проекция на 3. на Mτnb: m*dv/dt=ΣFkτ, m*dv/dt=ΣFkn, m*dv/dt=ΣFkb 3. 1) по заданному движению точки или системы определить силы, производящие это движение. 2) по заданным силам, действующим на точку или систему, определить движение этих объектов. 1) Решение первой основной задачи динамики. Пусть движение точки массой m задано координатным способом, т.е. заданы x = f1(t); y = f2(t); z = f3(t) Дифференцируя дважды по t и подставляя значения в уравнения (1): Модуль и направляющие косинусы равнодействующей найдем по формулам:
Если движение задано естественным способом: S = f(t) 2) Решение второй задачи динамики: В общем случае равнодействующая
x = f1(t,c1, c2, c3, c4, c5, c6) Чтобы выбрать из семейства одну определенную y = f2(t,c1, c2, c3, c4, c5, c6) траекторию, следует придать параметрам c1,…, c6 z = f3(t,c1, c2, c3, c4, c5, c6) конкретные значения. Их находят с помощью начальных условий. 4. Систему материальных точек или тел, движение(или равновесие) которой рассматривается, будем называть механической системой. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга. Их свойства:1. Геометрическая сумма всех внутренних сил системы =0(так как для любой пары точек системы имеет место третий закон динамики).2. Сумма моментов всех внутренних сил системы относительно любого центра или оси равняется 0(т.к. для всех точек системы m(F12)+m(F21)=0). Рассмотрим механическую систему, состоящую из
где
Систему уравнений (3.1) называют системой дифференциальных уравнений движения точек механической системы. Одна из основных задач механики состоит в том, чтобы, зная активные силы и связи, наложенные на систему, определить движение всех точек системы и определить реакции связей. Решение такой задачи связано с интегрированием системы уравнений (3.1) при заданных начальных условиях. Однако, прямое интегрирование системы (3.1) весьма сложно, что связано как с возможно большим числом этих уравнений, так и, в основном, с неопределенностью информации о внутренних силах. Во многих практически интересных случаях нет необходимости определять все интегралы системы (3.1), достаточно получить лишь некоторые из них. Это позволяют сделать общие теоремы динамики. Являясь прямым следствием уравнений (3.1), общие теоремы динамики связывают основные динамические величины, характеризующие движение системы, с приложенными к ней внешними силами. 5. 1) Количество движения (импульс тела) – векторная физическая величина, равная произведению массы тела на его скорость:
Импульс (количество движения) – одна из самых фундаментальных характеристик движения тела или системы тел. Запишем II закон Ньютона в другой форме, учитывая, что ускорение
Произведение силы на время ее действия равно приращению импульса тела (рис. 1):
Где
В проекциях на координатные оси будем иметь:
1) Пусть сумма всех внешних сил, действующих на замкнутую систему, равна нулю:
Тогда из уравнения 2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:
Тогда из уравнения Эти результаты и выражают закон сохранения количества движения системы: при любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы все время остается постоянным. 6. 1) центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы и Если в точках
В координатах:
Rвн→=M⋅ac→, где Rвн→ − векторная сумма всех внешних сил, M − масса системы материальных точек, ac→ − ускорение центра масс системы материальных точек. 7. 1)Момент количества движениякинетический момент, одна из мер механического движенияматериальной точки или системы. Для вычисления М. к. д. k материальной точки относительно центра О или оси z справедливы всеформулы, приведённые для вычисления момента силы, если в них заменить вектор F вектором количествадвижения (См. Количество движения) mv. Т. о., k o = [ r · mυ;], где r — радиус-вектор движущейся точки,проведённый из центра О, a kz равняется проекции вектора ko на ось z, проходящую через точку О. Изменение М. к. д. точки происходит под действием момента mo (F) приложенной силы и определяетсятеоремой об изменении М. к. д., выражаемой уравнением dko / dt = mo (F). Главный М. к. д. (или кинетический момент) механической системы относительно центра О или оси z равен соответственно геометрической или алгебраической сумме М. к. д. всех точек системы относительнотого же центра или оси, т. е. Ko = Σ koi, Kz = Σ kzi. Вектор Ko может быть определён его проекциями Kx, Ky, Kz на координатные оси. Для тела, вращающегося вокруг неподвижной оси z с угловой скоростью ω, K x = — I xzω, K y = — I yzω, K z = I zω, где lz — осевой, а Ixz, lyz — центробежные моменты инерции (См. Моментинерции). Если ось z является главной осью инерции для начала координат О, то Ko = I zω. 2) Во вращательном движении момент силы, действуя в течение определенного времени, создает импульс момента силы., Импульс момента силы — это мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).
где 8. 1) Механическая работа (более развёрнуто: Работа силы F за время Δt процесса γ(t)) — это физическая величина, являющаяся количественной характеристикой действия силы F на процесс γ(t), зависящая от численной величины и направления силы и от перемещения точки ее приложения
2) Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергиисистемы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени[1]. N=A/t 3)Кинетическая энергия механической системы Кинетической энергией механической системы называется сумма кинетических энергий всех точек этой системы: T = ∑ mkvk2 / 2, где mk и vk - масса и скорость k -й материальной точки, принадлежащей данной системе.4) Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ внешних и внутренних сил, приложенных к точкам системы, на том же перемещении.
9. ответ 7 ( 3 ) 10) Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы
Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач. Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:
Кинетическая энергия – скалярная и всегда положительная величина. Найдем формулы для вычисления кинетической энергии тела в разных случаях движения. 1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки Vi=VC
или
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит. 2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.1), то скорость любой его точки
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
т.е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.
Рис.1
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.2)
или, окончательно,
где
Рис.2
3. Плоскопараллельное движение. При этом движении скорости всех точек тела в каждый момент времени распределены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр скоростей Р (рис.1). Следовательно
где
Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной скинетической энергией вращательного движения вокруг центра масс. 4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига. Рассмотрим движение материальной системы как сумму двух движений (рис.3). Переносного – поступательного движения вместе с центром масс С и относительного – движения относительно поступательно движущихся вместе с центром масс осей x 1, y 1, z 1. Тогда скорость точек
Рис.3
По определению центра масс его радиус-вектор в подвижной системе
Поэтому, окончательно, кинетическая энергия системы
Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс. В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного – поступательного вместе с центром масс С и относительного – вращения вокруг точки С), по теореме Кенига (1) получим
где Ix, Iy, Iz – главные центральные оси инерции тела. 11) Теоре́ма Кёнига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра массКинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:
12) 1) Потенциальная энергия
где
2)
|

 2-й: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
2-й: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
 — ускорение тела,
— ускорение тела,  — силы, приложенные к материальной точке, а
— силы, приложенные к материальной точке, а  — её масса, или
— её масса, или

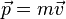 — импульс (количество движения) точки,
— импульс (количество движения) точки,  — её скорость, а
— её скорость, а  — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени[7][8][9].
— время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени[7][8][9].

 .
. ,
,  и
и  , получим дифференциальные уравнения движения точки в декартовых координатах:
, получим дифференциальные уравнения движения точки в декартовых координатах: ;
;  i;
i;  ,
, ;
;  i;
i;  .
. , а скорость точки в данный момент – начальной скоростью
, а скорость точки в данный момент – начальной скоростью  .
. ,
,  ) и показать все действующие на точку силы;
) и показать все действующие на точку силы;
 ;
;  .
. ,
,  ,
,  .
. ;
;  ;
;  ;
; 
 ,
,  ,
,  ,
,  ,
, 
 будет зависеть от времени, координат точки и ее скорости.
будет зависеть от времени, координат точки и ее скорости.



 после интегрирования
после интегрирования материальных точек. Для каждой точки системы в инерциальной системе отсчета справедлив второй закон Ньютона:
материальных точек. Для каждой точки системы в инерциальной системе отсчета справедлив второй закон Ньютона: (3.1)
(3.1) – масса точки с номером
– масса точки с номером  ;
;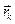 – ее радиус–вектор;
– ее радиус–вектор; – равнодействующая всех внешних сил как активных, так и реакций связей, действующих на точку с номером
– равнодействующая всех внешних сил как активных, так и реакций связей, действующих на точку с номером  – равнодействующая всех внутренних сил, действующих на точку с номером
– равнодействующая всех внутренних сил, действующих на точку с номером 
 Тогда
Тогда  следовательно
следовательно

 - импульс силы, который показывает, что результат действия силы зависит не только от ее значения, но и от продолжительности ее действия.
- импульс силы, который показывает, что результат действия силы зависит не только от ее значения, но и от продолжительности ее действия. 2) И́мпульс си́лы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении). За конечный промежуток времени эта величина равна определённому интегралу от элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.
2) И́мпульс си́лы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении). За конечный промежуток времени эта величина равна определённому интегралу от элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время. .3) изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
.3) изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени. . 4) Из теоремы об изменении количества движения системы можно получить следующие важные следствия:
. 4) Из теоремы об изменении количества движения системы можно получить следующие важные следствия:
 следует, что Q=
следует, что Q=  =const. Таким образом, если сумма всех внешних сил, действующих на замкнутую систему, равна нулю, то вектор количества движения (импульса) системы будет постоянен по модулю и направлению.
=const. Таким образом, если сумма всех внешних сил, действующих на замкнутую систему, равна нулю, то вектор количества движения (импульса) системы будет постоянен по модулю и направлению.
 следует, что при этом Qx=const. Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения (импульса) системы на эту ось есть величина постоянная.
следует, что при этом Qx=const. Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения (импульса) системы на эту ось есть величина постоянная. (с радиусами-векторами
(с радиусами-векторами  ) сосредоточены массы
) сосредоточены массы  то радиус-вектор центра масс
то радиус-вектор центра масс


 2)
2)  или
или  .3) При движении системы материальных точек ее центр масс движется так, как двигалась бы материальная точка, помещенная в центре масс, если бы в ней были сконцентрированы массы всех точек системы и к ней были бы приложены все внешние силы, действующие на точки системы:
.3) При движении системы материальных точек ее центр масс движется так, как двигалась бы материальная точка, помещенная в центре масс, если бы в ней были сконцентрированы массы всех точек системы и к ней были бы приложены все внешние силы, действующие на точки системы: где
где  — векторное произведение. 3) С помощью теоремы об изменении кинетического момента решают задачи по термеху на нахождения угловой скорости тела, вращающегося вокруг неподвижной опоры, к которому приложены внешние силы и (или) по которому движется материальная точка. Как и в других теоремах динамики, решение задачи сводиться к составлению выражения в соответствии с этой теоремой – теоремой об изменении кинетического момента (тела или системы тел):
— векторное произведение. 3) С помощью теоремы об изменении кинетического момента решают задачи по термеху на нахождения угловой скорости тела, вращающегося вокруг неподвижной опоры, к которому приложены внешние силы и (или) по которому движется материальная точка. Как и в других теоремах динамики, решение задачи сводиться к составлению выражения в соответствии с этой теоремой – теоремой об изменении кинетического момента (тела или системы тел): 4).Формулировка закона: если при движении системы сумма моментов внешних сил относительно неподвижной оси
4).Формулировка закона: если при движении системы сумма моментов внешних сил относительно неподвижной оси  равна нулю, то кинетический момент системы относительно этой оси есть величина постоянная, т. е. если
равна нулю, то кинетический момент системы относительно этой оси есть величина постоянная, т. е. если , то
, то 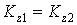 , (2.5)
, (2.5)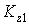 и
и  – кинетические моменты в 1-м и 2-м положениях системы.
– кинетические моменты в 1-м и 2-м положениях системы. .. Работа силы на конечном перемещении определяется как интегральная сумма элементарных Работа при перемещении M 0 M 1 выражается криволинейным интегралом:
.. Работа силы на конечном перемещении определяется как интегральная сумма элементарных Работа при перемещении M 0 M 1 выражается криволинейным интегралом: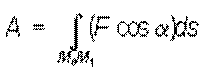 или
или 
 самые два последние выражения!!!!!
самые два последние выражения!!!!!



 где
где  - расстояние точки от оси вращения, а
- расстояние точки от оси вращения, а  - угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:
- угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:




 – моменты инерции тела относительно главных осей инерции x 1, y 1, z 1 в неподвижной точке О;
– моменты инерции тела относительно главных осей инерции x 1, y 1, z 1 в неподвижной точке О;  – проекции вектора мгновенной угловой скорости
– проекции вектора мгновенной угловой скорости  на эти оси.
на эти оси.

 - момент инерции тела относительно названной выше оси,
- момент инерции тела относительно названной выше оси,  - угловая скорость тела. Величина
- угловая скорость тела. Величина  , относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса-Штейнера
, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса-Штейнера  , где d=PC. Подставим это выражение для
, где d=PC. Подставим это выражение для  . Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно,
. Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно,  , где
, где  - скорость центра масс С, окончательно найдем:
- скорость центра масс С, окончательно найдем:
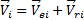 . Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны
. Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны  . Значит,
. Значит,  и кинетическая энергия будет
и кинетическая энергия будет


 (центр масс находится в начале координат), значит, и
(центр масс находится в начале координат), значит, и  . Производная по времени от этой суммы также равна нулю:
. Производная по времени от этой суммы также равна нулю:


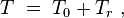 где
где  — полная кинетическая энергия системы,
— полная кинетическая энергия системы,  — кинетическая энергия движения центра масс,
— кинетическая энергия движения центра масс,  — относительная кинетическая энергия системы[2].
— относительная кинетическая энергия системы[2]. — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в полеконсервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении[1]. Потенциальная энергия тела
— скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в полеконсервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении[1]. Потенциальная энергия тела  в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
 — ускорение свободного падения,
— ускорение свободного падения, 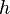 — высота положения центра масс тела над произвольно выбранным нулевым уровнем. 2) В физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем. 2) В физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0. — работа консервативных сил по произвольному замкнутому контуру равна 0;
— работа консервативных сил по произвольному замкнутому контуру равна 0;


