Активные и реактивные силы. Идеальные связи. Основные случаи идеальных связей.
Активные и реактивные силы являются внешними силами (нагрузками), вызывающими деформацию изгиба в балке. Принцип Даламбера формулируется так: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия. Как было сказано выше, внешними нагрузками балки являются активные и реактивные силы и моменты. Решая задачу первым способом, мы учитывали только фактически действующие на тело активные и реактивные силы и составили шесть всеобщих уравнений движения, связывающих проекции этих сил с массами и с проекциями ускорений частиц тела. Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией - осью, к которой приложены активные и реактивные силы. Пусть все активные и реактивные силы и массы механизма приведены к одному из его звеньев. Расчеты с учетом инерционных нагрузок ведутся известным из теоретической механики методом кинетостатики, основанном на принципе Даламбера. Согласно этому принципу все активные и реактивные силы, приложенные к телу, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия. Таким образом, задачи динамики и сопромата решаются методами статики.
Возможная работа - элементраная работа силы на возможном перемещении. dA=Fdr - элементарная работа силы (F и r - векторы) Для системы:
Если у какой-то связи Если вся сумма Примеры идеальных связей: внутренние связи в абсолютно твердых телах; абсолютно гладкие поверхности; шарниры без трения; нерастяжимые нити; закрепленные точки; качение без скольжения. Примеры идеальных связей: 1. Наложенная на материальную точку связь в виде гладкой поверхности (неподвижной или деформирующейся с течением времени), по которой должна двигаться точка (здесь возможные перемещения лежат в касательной плоскости к данной поверхности, а реакция связи этой плоскости ортогональна, так что скалярное произведение равно нулю). 2. Внутренние связи в абсолютно твёрдом теле, обеспечивающие постоянство расстояний между текущими положениями точек тела. 3. Контакт двух абсолютно твёрдых тел, соприкасающихся при движении гладкими поверхностями. 4. Контакт двух абсолютно твёрдых тел, соприкасающихся при движении абсолютно шероховатыми поверхностями.
|

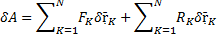
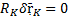 (RK тоже вектор), то связь называется идеальной.
(RK тоже вектор), то связь называется идеальной.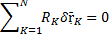 , то механическая система с идеальными связями.
, то механическая система с идеальными связями.


